题目内容
17.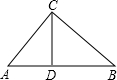 如图,在Rt△ABC中,∠ACB=90°,AB=$\sqrt{13}$,BC=2,则这个直角三角形的面积为( )
如图,在Rt△ABC中,∠ACB=90°,AB=$\sqrt{13}$,BC=2,则这个直角三角形的面积为( )| A. | 3 | B. | 6 | C. | $\sqrt{13}$ | D. | $\frac{1}{2}$$\sqrt{13}$ |
分析 利用勾股定理易求AC的长,进而可求出这个直角三角形的面积.
解答 解:
∵在Rt△ABC中,∠ACB=90°,AB=$\sqrt{13}$,BC=2,
∴AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=3,
∴这个直角三角形的面积=$\frac{1}{2}$AC•BC=3,
故选A.
点评 本题考查了勾股定理的运用,解题的关键是要熟知直角三角形的性质及其面积公式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.不等式1-2x≤5的解集在数轴上表示为( )
| A. |  | B. |  | C. |  | D. | 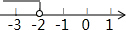 |
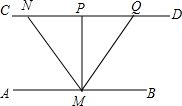 请你将下面的证明补充完整,并在括号内填写推理依据.
请你将下面的证明补充完整,并在括号内填写推理依据. 如图,点P沿半圆弧AB从A向B匀速运动,若运动时间为t,扇形OAP的面积为s,则s与t的函数图象大致是( )
如图,点P沿半圆弧AB从A向B匀速运动,若运动时间为t,扇形OAP的面积为s,则s与t的函数图象大致是( )


