题目内容
3.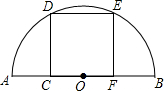 如图,在以AB为直径的半圆中,有一个边长为1的内接正方形CDEF.
如图,在以AB为直径的半圆中,有一个边长为1的内接正方形CDEF.(1)求证:AC=BF;
(2)小正方形MNGF,M在EF上,N点在⊙O上,G点在BF上,求MN的长.
分析 (1)连接OD,OE,则OD=OE,求证:OC=OF,可以转化为求证Rt△DOC≌Rt△EOF.
(2)连接ON,在Rt△OEF中勾股定理得到OE,然后在Rt△ONG中根据勾股定理,得到关于设正方形FGNK的边长为x的方程,就可以求出x的值.
解答 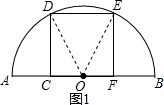 (1)证明:如图1,连接OD,OE,则OD=OE,
(1)证明:如图1,连接OD,OE,则OD=OE,
∵四边形CDEF为正方形,
∴CD=FE,∠DCO=∠EFO=90°,
∴在Rt△DOC和Rt△EOF中,
$\left\{\begin{array}{l}{OD=OE}\\{CD=FE}\end{array}\right.$,
∴Rt△DOC≌Rt△EOF,
∴OC=OF,
∵OA=OB,
∴AC=BF;
(2)解:连接ON,设正方形FGNM的边长为x,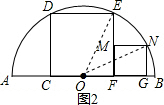
由已知及(1)可得EF=1,OF=$\frac{1}{2}$
在Rt△OEF中,OE2=OF2+EF2=($\frac{1}{2}$)2+12=$\frac{\sqrt{5}}{2}$,
在Rt△ONG中,ON2=OG2+GN2,OE=ON,
∴1=($\frac{1}{2}$+x)2+x2,整理得x2+x-2=0.
解得x1=-$\frac{1+\sqrt{7}}{4}$(不合题意,舍去),x2=$\frac{\sqrt{7}-1}{4}$,
∴MN=$\frac{\sqrt{7}-1}{4}$.
点评 本题考查了垂径定理,正方形的性质,勾股定理,全等三角形的判定和性质,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
13.下列四个数中,最大的数是( )
| A. | (-2)3 | B. | -23 | C. | -|-2|3 | D. | -(-2)3 |
14.下列命题中,真命题的个数为( )
①顶点在圆周上的角是圆周角;
②圆内接平行四边形一定是矩形;
③90°的圆周角所对的弦是直径;
④平分弦的直径垂直于弦;
⑤圆周角相等,则它们所对的弧也相等;
⑥同弧或等弧所对的圆周角相等.
①顶点在圆周上的角是圆周角;
②圆内接平行四边形一定是矩形;
③90°的圆周角所对的弦是直径;
④平分弦的直径垂直于弦;
⑤圆周角相等,则它们所对的弧也相等;
⑥同弧或等弧所对的圆周角相等.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
12.初一(3)班有m个同学,若每5人分成一个学习小组,则有2个小组各少1人,用代数式表示这个班级分成的学习小组数为( )
| A. | $\frac{m+2}{5}$ | B. | $\frac{m-2}{5}$ | C. | $\frac{m}{5}-2$ | D. | $\frac{m}{5}+2$ |
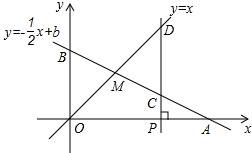 如图所示,已知函数y=-$\frac{1}{2}$x+b的图象与x轴、y轴分别交于点A、B,与函数y=x的图象交于点M,点M的横坐标为2,在x轴上有一点P(a,0)(其中a>2),过点P作x轴的垂线,分别交函数y=-$\frac{1}{2}$x+b和y=x的图象于点C,D.
如图所示,已知函数y=-$\frac{1}{2}$x+b的图象与x轴、y轴分别交于点A、B,与函数y=x的图象交于点M,点M的横坐标为2,在x轴上有一点P(a,0)(其中a>2),过点P作x轴的垂线,分别交函数y=-$\frac{1}{2}$x+b和y=x的图象于点C,D.  如图,BC⊥AD于C,AC=BC,点E在BC上,且AE=BD.
如图,BC⊥AD于C,AC=BC,点E在BC上,且AE=BD. 如图,已知点A、F、C、D在同一直线上,DE=AB,EF=BC,CD=AF,求证:BC∥EF.
如图,已知点A、F、C、D在同一直线上,DE=AB,EF=BC,CD=AF,求证:BC∥EF.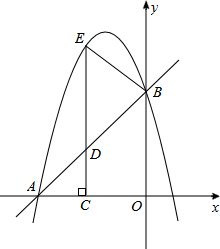 如图,在平面直角坐标系xOy中,直线y=x+4与x轴、y轴分别交于点A,B,抛物线y=-x2+bx+c经过A、B两点,D(m,m+4)为直线AB上一动点,过点D作x轴的垂线,垂足为点C,CD的延长线交抛物线于点E,连接BE.
如图,在平面直角坐标系xOy中,直线y=x+4与x轴、y轴分别交于点A,B,抛物线y=-x2+bx+c经过A、B两点,D(m,m+4)为直线AB上一动点,过点D作x轴的垂线,垂足为点C,CD的延长线交抛物线于点E,连接BE.