题目内容
18.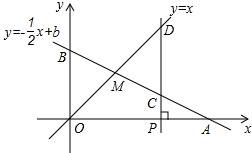 如图所示,已知函数y=-$\frac{1}{2}$x+b的图象与x轴、y轴分别交于点A、B,与函数y=x的图象交于点M,点M的横坐标为2,在x轴上有一点P(a,0)(其中a>2),过点P作x轴的垂线,分别交函数y=-$\frac{1}{2}$x+b和y=x的图象于点C,D.
如图所示,已知函数y=-$\frac{1}{2}$x+b的图象与x轴、y轴分别交于点A、B,与函数y=x的图象交于点M,点M的横坐标为2,在x轴上有一点P(a,0)(其中a>2),过点P作x轴的垂线,分别交函数y=-$\frac{1}{2}$x+b和y=x的图象于点C,D. (1)求直线AB的函数关系式;
(2)若OB=CD,求a的值;
(3)在(2)的条件下,求四边形OMCP的面积.
分析 (1)把x=2代入y=x中,得出y=2,再把x=2,y=2代入y=-$\frac{1}{2}$x+b解答即可;
(2)先确定B点坐标为(0,3),则OB=CD=3,再表示出C点坐标为(a,-$\frac{1}{2}$a+3),D点坐标为(a,a),所以a-(-$\frac{1}{2}$a+3)=3,然后解方程即可;
(3)根据四边形OMCP的面积等于△OMF的面积+梯形MFCP的面积.
解答 解:(1)把x=2代入y=x中,可得:y=2,
把x=2,y=2代入y=-$\frac{1}{2}$x+b,可得:b=3,
所以直线AB的函数关系式是y=-0.5x+3;
(2)把x=0代入y=-0.5x+3得y=3,
∴B点坐标为(0,3),
∵CD=OB,
∴CD=3,
∵PC⊥x轴,
∴C点坐标为(a,-$\frac{1}{2}$a+3),D点坐标为(a,a)
∴a-(-$\frac{1}{2}$a+3)=3,
∴a=4;
(3)过点M作MF⊥OA,如图:
点C的坐标为(4,1),D坐标为(4,4),
四边形OMCP的面积=△OMF的面积+梯形MFCP的面积=$\frac{1}{2}×2×2+\frac{1}{2}×(2+1)×2=5$.
点评 本题考查了两条直线相交或平行问题:两条直线的交点坐标,就是由这两条直线相对应的一次函数表达式所组成的二元一次方程组的解;若两条直线是平行的关系,那么他们的自变量系数相同,即k值相同.

练习册系列答案
相关题目
9.下列各组数据中,可以作为直角三角形三边长的有( )
①1,2,3;②12a,5a,13a(其中a为正数);③12,22,32;④$\sqrt{2}$,$\sqrt{3}$,$\sqrt{5}$.
①1,2,3;②12a,5a,13a(其中a为正数);③12,22,32;④$\sqrt{2}$,$\sqrt{3}$,$\sqrt{5}$.
| A. | 1组 | B. | 2组 | C. | 3组 | D. | 4组 |
6.某移动电话公司给用户提供了各种手机资源套餐,其中两个如表所列:
(1)如果某用户某月国内主叫通话总时长为x分钟,使用国内数据流量为y兆(字节),请分别写出两种套餐收费方式下用户应该支付的费用(假定150≤x≤350,y≥30).
(2)如果某用户某月国内主叫通话总时长为250分钟,使用国内数据流量为90兆(字节),上述两种套餐中他选哪一种较为合算?
| 套餐使用费(单位:元/月) | 套餐内包含国内主叫通话时长(单位:分钟) | 套餐外国内主叫通话单价(单位:元/分钟) | 国内被叫 | 套餐内包含国内数据流量(单位:兆) | 套餐外国内数据流量单价(单位:元/兆) |
| 58 | 150 | 0.25 | 免费 | 30 | 0.50 |
| 88 | 350 | 0.19 | 免费 | 30 | 0.50 |
(2)如果某用户某月国内主叫通话总时长为250分钟,使用国内数据流量为90兆(字节),上述两种套餐中他选哪一种较为合算?
 如图,在△ABC中,AB=AC=2,点P在BC上.若点P为BC的中点,则m=AP2+BP•PC的值为4;若BC边上有100个不同的点P1,P2,…,P100,且mi=APi2+BPi•PiC(i=1,2,…,100),则m=m1+m2+…+m100 的值为400.
如图,在△ABC中,AB=AC=2,点P在BC上.若点P为BC的中点,则m=AP2+BP•PC的值为4;若BC边上有100个不同的点P1,P2,…,P100,且mi=APi2+BPi•PiC(i=1,2,…,100),则m=m1+m2+…+m100 的值为400.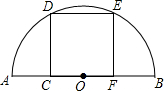 如图,在以AB为直径的半圆中,有一个边长为1的内接正方形CDEF.
如图,在以AB为直径的半圆中,有一个边长为1的内接正方形CDEF.