题目内容
4．在平面直角坐标系中，抛物线y=x2+2x-3与x轴的交点个数是（ ）| A． | 0 | B． | 1 | C． | 2 | D． | 3 |
分析 令y=0，得到关于x的一元二次方程x2+2x-3=0，然后根据△判断出方程的解得个数即可．
解答 解：令y=0得：x2+2x-3=0，
∵△=b2-4ac=22-4×1×（-3）=4+12=16＞0，
∴抛物线与x轴有两个交点．
故选：C．
点评 本题主要考查的是抛物线与x轴的交点，将函数问题转化为方程问题是解题的关键．
练习册系列答案
活力课时同步练习册系列答案
相关题目
15．下列图形是相似图形的是（ ）
| A． | 所有矩形 | B． | 所有菱形 | C． | 所有直角三角形 | D． | 所有正六边形 |
如图，AB地半圆O的直径，AD和BC是它的两条切线，切点分别为A、B，CO平分∠BCD．
19．抛物线y=3x2+2x的开口方向是（ ）
| A． | 向上 | B． | 向下 | C． | 向左 | D． | 向右 |
如图所示，已知AD平分∠CAE，∠B=∠1，证明：AD∥BC．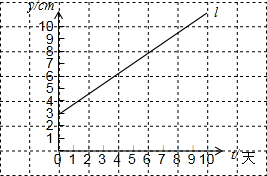
如图，某植物t天后的高度为ycm，l放映了y与t之间的关系，根据图象回答下列问题：