题目内容
20．若3x-5y=0，则$\frac{x}{y}$=$\frac{5}{3}$．分析 由5x-3y=0，移项即可得：5x=3y，根据比例的性质，即可解答．
解答 解：3x-5y=0，
3x=5y，
$\frac{x}{y}=\frac{5}{3}$．
故答案为：$\frac{5}{3}$．
点评 此题考查了比例的性质．题目比较简单，注意掌握比例变形是解此题的关键．
练习册系列答案
云南师大附小一线名师提优作业系列答案
冲刺100分单元优化练考卷系列答案
相关题目
10．
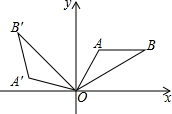如图，将△OAB绕原点0逆时针旋转105°到△OA′B′的位置，若AB∥x轴，OA=AB，OB=2，∠A=120°，则点B′的坐标为（ ）
如图，将△OAB绕原点0逆时针旋转105°到△OA′B′的位置，若AB∥x轴，OA=AB，OB=2，∠A=120°，则点B′的坐标为（ ）| A． | （-2，2$\sqrt{2}$） | B． | （-2$\sqrt{2}$，2） | C． | （$\sqrt{2}$，-$\sqrt{2}$） | D． | （-$\sqrt{2}$，$\sqrt{2}$） |
8．
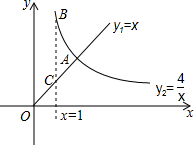如图，直线和双曲线分别是函数y1=x（x≥0），y2=$\frac{4}{x}$（x＞0）的图象，则以下结论：
①两函数图象的交点A的坐标为（2，2）
②当x＞2时，y1＜y2
③当x=1时，BC=3
④当x逐渐增大时，y1随着x的增大而增大，y2随着x的增大而减小．
其中正确结论的序号是（ ）
如图，直线和双曲线分别是函数y1=x（x≥0），y2=$\frac{4}{x}$（x＞0）的图象，则以下结论：①两函数图象的交点A的坐标为（2，2）
②当x＞2时，y1＜y2
③当x=1时，BC=3
④当x逐渐增大时，y1随着x的增大而增大，y2随着x的增大而减小．
其中正确结论的序号是（ ）
| A． | ①③④ | B． | ①②③ | C． | ②③④ | D． | ①②③④ |
15．若$\frac{|x|-2}{{x}^{2}-x-2}$=0，则x等于（ ）
| A． | 2 | B． | -2 | C． | ±2 | D． | 0 |
5．在1，0，-2，3这四个数中，比0小的数是（ ）
| A． | 1 | B． | 0 | C． | -2 | D． | 3 |
10．一元二次方程x（x-5）=0的解是（ ）
| A． | x=0或x=5 | B． | x=0 | C． | x=5 | D． | x=0或x=-5 |