题目内容
5.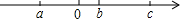 已知数a,b,c的大小关系如图所示,则下列各式:
已知数a,b,c的大小关系如图所示,则下列各式:①abc>0;②a+b-c>0;③$\frac{a}{|a|}+\frac{b}{|b|}+\frac{|c|}{c}=1$;④bc-a>0;⑤|a-b|-|c+a|+|b-c|=-2a,其中正确的有( )个.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 先根据各点在数轴上的位置判断出其符号及绝对值的大小,再对各小题进行分析即可.
解答 解:由图可知a<0<b<c.
①∵a<0<b<c,∴abc<0,故本小题错误;
②∵|a|>b,c>0,∵a+b<0,∴a+b-c<0,故本小题错误;
③∵a<0<b<c,∴$\frac{a}{\left|a\right|}$=-1,$\frac{b}{\left|b\right|}$=$\frac{c}{\left|c\right|}$=1,∴$\frac{a}{\left|a\right|}$+$\frac{b}{\left|b\right|}$+$\frac{c}{\left|c\right|}$=1,故本小题正确;
④∵bc>0,a<0,∴bc-a>0,故本小题正确;
⑤∵a-b<0,c+a>0,b-c<0,∴原式=b-a-(c+a)+(c-b)=b-a-c-a+c-b=-2a,故本小题正确.
故选C.
点评 本题考查的是有理数的混合运算及整式的加减,先根据题意判断出a、b、c的符号是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.下列说法其中正确的个数有( )
①能够完全重合的两个三角形是全等三角形;
②通过旋转得到的两个图形全等,全等的两个图形旋转后一定能重合;
③大小相同的两个图形是全等图形;
④一个图形经过平移、翻折、旋转后,得到的图形一定与原图形全等.
①能够完全重合的两个三角形是全等三角形;
②通过旋转得到的两个图形全等,全等的两个图形旋转后一定能重合;
③大小相同的两个图形是全等图形;
④一个图形经过平移、翻折、旋转后,得到的图形一定与原图形全等.
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
13.与数轴上的点一一对应的数是( )
| A. | 分数 | B. | 有理数 | C. | 无理数 | D. | 实数 |
17.下列各组条件中,能够判定△ABC≌△DEF的是( )
| A. | ∠A=∠D,∠B=∠E,∠C=∠F | B. | AB=DE,BC=EF,∠A=∠D | ||
| C. | ∠B=∠E=90°,BC=EF,AC=DF | D. | ∠A=∠D,AB=DF,∠B=∠E |
 如图,线段AB的长为1,C在AB上,D在AC上,且AC2=BC•AB,AD2=CD•AC,AE2=DE•AD,则AE的长为$\sqrt{5}$-2.
如图,线段AB的长为1,C在AB上,D在AC上,且AC2=BC•AB,AD2=CD•AC,AE2=DE•AD,则AE的长为$\sqrt{5}$-2.