题目内容
20.已知x1,x2是一元二次方程x2=2x+1的两个根,则$\frac{1}{{x}_{1}}+\frac{1}{{x}_{2}}$的值为-2.分析 先把方程化为一般式,再根据根与系数的关系得到x1+x2=2,x1x2=-1,然后利用通分得到$\frac{1}{{x}_{1}}+\frac{1}{{x}_{2}}$=$\frac{{x}_{1}+{x}_{2}}{{x}_{1}{x}_{2}}$,再利用整体代入的方法计算即可.
解答 解:x2-2x-1=0,
根据题意得x1+x2=2,x1x2=-1,
$\frac{1}{{x}_{1}}+\frac{1}{{x}_{2}}$=$\frac{{x}_{1}+{x}_{2}}{{x}_{1}{x}_{2}}$=$\frac{2}{-1}$=-2.
故答案为-2.
点评 若本题考查了根与系数的关系:若:x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案
相关题目
8.若有理数m,n满足mn>0,且m+n<0,则下列说法正确的是( )
| A. | m,n可能一正一负 | B. | m,n都是正数 | ||
| C. | m,n都是负数 | D. | m,n中可能有一个为0 |
15.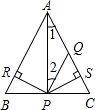 如图,已知在△ABC中,PR⊥AB于R,PS⊥AC于S,PR=PS,∠1=∠2,则四个结论:①AR=AS;②PQ∥AB;③△BPR≌△CPS;④BP=CP中( )
如图,已知在△ABC中,PR⊥AB于R,PS⊥AC于S,PR=PS,∠1=∠2,则四个结论:①AR=AS;②PQ∥AB;③△BPR≌△CPS;④BP=CP中( )
 如图,已知在△ABC中,PR⊥AB于R,PS⊥AC于S,PR=PS,∠1=∠2,则四个结论:①AR=AS;②PQ∥AB;③△BPR≌△CPS;④BP=CP中( )
如图,已知在△ABC中,PR⊥AB于R,PS⊥AC于S,PR=PS,∠1=∠2,则四个结论:①AR=AS;②PQ∥AB;③△BPR≌△CPS;④BP=CP中( )| A. | 全部正确 | B. | 仅①②正确 | C. | 仅①正确 | D. | 仅①④正确 |
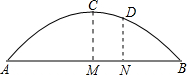 如图,一石拱桥呈抛物线状,已知石拱跨度AB为40米,拱高CM为16米,把桥拱看作一个二次函数的图象,建立适当的坐标系.
如图,一石拱桥呈抛物线状,已知石拱跨度AB为40米,拱高CM为16米,把桥拱看作一个二次函数的图象,建立适当的坐标系.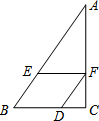 如图,已知四边形BDEF是平行四边形,AE=5,BE=2,DC=1,求EF的长度.
如图,已知四边形BDEF是平行四边形,AE=5,BE=2,DC=1,求EF的长度.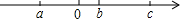 已知数a,b,c的大小关系如图所示,则下列各式:
已知数a,b,c的大小关系如图所示,则下列各式: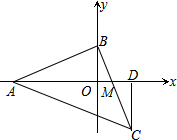 如图,等腰Rt△ABC中,∠ABC=90°,AB=BC.点A、B分别在坐标轴上,且x轴恰好平分∠BAC,BC交x轴于点M,过C点作CD⊥x轴于点D,则$\frac{CD}{AM}$的值为$\frac{1}{2}$.
如图,等腰Rt△ABC中,∠ABC=90°,AB=BC.点A、B分别在坐标轴上,且x轴恰好平分∠BAC,BC交x轴于点M,过C点作CD⊥x轴于点D,则$\frac{CD}{AM}$的值为$\frac{1}{2}$.