题目内容
13.(1)因为(x+$\frac{1}{x}$)2=x2+$\frac{1}{{x}^{2}}$+2,所有x2+$\frac{1}{{x}^{2}}$=(x+$\frac{1}{x}$)2-2,因为(x-$\frac{1}{x}$)2=x2+$\frac{1}{{x}^{2}}$-2,所有x2+$\frac{1}{{x}^{2}}$=(x-$\frac{1}{x}$)2+2;
(2)已知x+$\frac{1}{x}$=5,求下列各式的值:①x2+$\frac{1}{{x}^{2}}$;②(x-$\frac{1}{x}$)2.
分析 (1)根据完全平方公式可得(x+$\frac{1}{x}$)2与x2+$\frac{1}{{x}^{2}}$,(x-$\frac{1}{x}$)2与x2+$\frac{1}{{x}^{2}}$之间的关系;
(2)根据(1)的变形代入计算即可求解.
解答 解:(1)因为(x+$\frac{1}{x}$)2=x2+$\frac{1}{{x}^{2}}$+2,所有x2+$\frac{1}{{x}^{2}}$=(x+$\frac{1}{x}$)2-2,
因为(x-$\frac{1}{x}$)2=x2+$\frac{1}{{x}^{2}}$-2,所有x2+$\frac{1}{{x}^{2}}$=(x-$\frac{1}{x}$)2+2;
(2)∵x+$\frac{1}{x}$=5,
∴①x2+$\frac{1}{{x}^{2}}$
=(x+$\frac{1}{x}$)2-2
=25-2
=23;
②(x-$\frac{1}{x}$)2
=x2+$\frac{1}{{x}^{2}}$-2
=23-2
=21.
故答案为:x2+$\frac{1}{{x}^{2}}$+2,(x+$\frac{1}{x}$)2-2;x2+$\frac{1}{{x}^{2}}$-2,(x-$\frac{1}{x}$)2+2.
点评 本题主要考查完全平方公式,熟记公式的几个变形公式对解题大有帮助.

练习册系列答案
相关题目
2.已知关于x的一元二次方程x2+mx+n=0的两根为3和-4,则代数式x2-mx+n可分解为( )
| A. | (x-3)(x+4) | B. | (x+3)(x+4) | C. | (x+3)(x-4) | D. | (x-3)(x-4) |
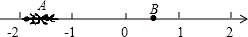 如图,一只蚂蚁从点A沿数轴向右爬行2个单位长度到达点B,点A表示-$\sqrt{2}$,设点B所表示的数为m.
如图,一只蚂蚁从点A沿数轴向右爬行2个单位长度到达点B,点A表示-$\sqrt{2}$,设点B所表示的数为m.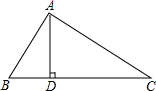 如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,∠B=2∠C,若CD=8,求AB+BD的值.
如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,∠B=2∠C,若CD=8,求AB+BD的值.