题目内容
5.利用等式的性质解下列方程:(1)2x+3=11;
(2)$\frac{3}{4}$x-1=$\frac{1}{2}$x+3;
(3)$\frac{1}{2}$x-1=6;
(4)-3x-1=5-6x.
分析 (1)利用等式的性质1变形为:2x=8,然后利用等式的性质2得到x=4;
(2)利用等式的性质1得到:$\frac{1}{4}x=4$,然后利用等式的性质2可得到x=16;
(3)利用等式的性质1得到$\frac{1}{2}x$=7,然后利用等式的性质2可得到x=14;
(4)利用等式的性质1得到3x=6,然后利用等式的性质2可得到x=2.
解答 解:(1)等式两边同时减3得:2x=8,等式两边同时除以2得x=4;
(2)等式两边同时减$\frac{1}{2}x$再加1得:$\frac{1}{4}x=4$,等式两边同时乘以4得x=16;
(3)等式两边同时加1得:$\frac{1}{2}x$=7,等式两边同时乘以2得x=14;
(4)等式两边同时加上6x+1得:3x=6,等式两边同时除以3得x=2.
点评 本题主要考查的是等式的性质,掌握等式的性质是解题的关键.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
20.某校艺体节上有34个同学同时参加男单、男双乒乓球比赛,正好用了12张球台,问男单、男双各几桌?若设男单x桌,男双y桌,所列方程组正确的是( )
| A. | $\left\{\begin{array}{l}{x+y=34}\\{x-y=12}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=12}\\{x+2y=34}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x+y=12}\\{2x+4y=34}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x-y=12}\\{2x+4y=34}\end{array}\right.$ |
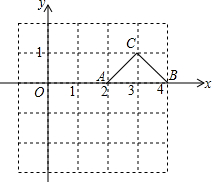 如图,在直角坐标系中,等腰直角三角形ABC的顶点A,B的坐标分别为A(2,0),B(4,0),将等腰直角三角形ABC沿x轴向左平移3个单位,使点A平移到点A′,在图中画出平移后的得到的△A′B′C′;并写出△A′B′C′的顶点坐标.
如图,在直角坐标系中,等腰直角三角形ABC的顶点A,B的坐标分别为A(2,0),B(4,0),将等腰直角三角形ABC沿x轴向左平移3个单位,使点A平移到点A′,在图中画出平移后的得到的△A′B′C′;并写出△A′B′C′的顶点坐标. 如图,在Rt△ABC中,∠C=90°,cosB=$\frac{5}{13}$,BC=10,求AB和sinA.
如图,在Rt△ABC中,∠C=90°,cosB=$\frac{5}{13}$,BC=10,求AB和sinA.