题目内容
4．
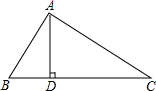如图，在Rt△ABC中，∠BAC=90°，AD⊥BC于点D，∠B=2∠C，若CD=8，求AB+BD的值．
分析 由三角形内角和定理求得∠B=60°，∠C=30°．在图中的直角△ABD和直角△ABC中，利用30度角所对的直角边等于斜边的一半进行解答．
解答 解：如图，∵在Rt△ABC中，∠BAC=90°，∠B=2∠C，
∴∠B=60°，∠C=30°．
又∵AD⊥BC于点D，
∴∠BAD=∠C=30°，
∴在直角△ABD中，AB=2BD．在直角△ABC中，AB=$\frac{1}{2}$BC，
∴2BD=$\frac{1}{2}$BC，即2BD=$\frac{1}{2}$（BD+CD）．
又CD=8，
∴2BD=$\frac{1}{2}$（BD+8），则BD=$\frac{8}{3}$，
故AB+BD=2BD+BD=3BD=8．
点评 本题考查了含30度角的直角三角形．在直角三角形中，30°角所对的直角边等于斜边的一半．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
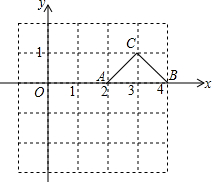如图，在直角坐标系中，等腰直角三角形ABC的顶点A，B的坐标分别为A（2，0），B（4，0），将等腰直角三角形ABC沿x轴向左平移3个单位，使点A平移到点A′，在图中画出平移后的得到的△A′B′C′；并写出△A′B′C′的顶点坐标．
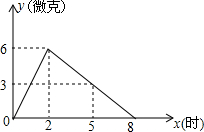某医药研究所开发了一种新药，在实验药效时发现，如果成人按规定剂量服用，每毫升血液中含药量y（微克）随时间x（时）的变化情况如图所示，那么当成人按规定剂量服药后，根据图象回答下列问题：
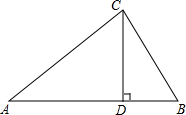如图，在R△ABC中，∠ACB=90°，CD⊥AB，AC=5，CD=3，求BC．