题目内容
17.两个相似三角形对应高的长分别为8cm和6cm,则它们的面积比为( )| A. | 4:3 | B. | $\sqrt{3}$:2 | C. | 2:$\sqrt{3}$ | D. | 16:9 |
分析 因为相似三角形的面积比等于相似比的平方,由此可得结果.
解答 解:∵两个相似三角形对应高的比是8:6=4:3,
∴它们的面积比是16:9,
故选D.
点评 考查了相似三角形的性质,利用相似三角形的面积比等于相似比的平方是解答此题的关键.

练习册系列答案
 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
7.如果一次函数y=kx+2k+2的图象经过第一、二、三象限,则k的取值范围是( )
| A. | k>0 | B. | k$>-\frac{1}{2}$ | C. | k<0 | D. | -$\frac{1}{2}$<k<0 |
8.已知?ABCD中,AC、BD交于点O.下列结论中,不一定成立的是( )
| A. | ?ABCD关于点O对称 | B. | OA=OC | ||
| C. | AC=BD | D. | ∠B=∠D |
5.在以下实数:-$\sqrt{2}$,$\sqrt{16}$,π,3.1411,8,0.020020002…中,无理数有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
12.不等式组$\left\{\begin{array}{l}x-1>0\\ x-3<0\end{array}\right.$的解集是( )
| A. | x>1 | B. | x<3 | C. | 1<x<3 | D. | 无解 |
9.如图图形中,既是中心对称图形又是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
7.点A(x,y)在某反比例函数的图象上,xy=4,则此函数的表达式为( )
| A. | y=$\frac{4}{x}$ | B. | y=$\frac{8}{x}$ | C. | y=-$\frac{8}{x}$ | D. | y=-$\frac{4}{x}$ |
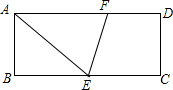 如图,在矩形ABCD中,E为BC边的中点,∠AEC的平分线交AD边于点F,若AB=3,AD=8,则FD的长为( )
如图,在矩形ABCD中,E为BC边的中点,∠AEC的平分线交AD边于点F,若AB=3,AD=8,则FD的长为( )