题目内容
4.解方程组(1)$\left\{\begin{array}{l}{y=4x-3}\\{3x+2y=5}\end{array}\right.$
(2)$\left\{\begin{array}{l}{2x+3y=7}\\{3x+y=7}\end{array}\right.$.
分析 根据二元一次方程组的解法即可求出答案.
解答 解:(1)$\left\{\begin{array}{l}{y=4x-3①}\\{3x+2y=5②}\end{array}\right.$
把①代入②中,3x+2(4x-3)=5
x=1
将x=1代入①中,
y=4×1-3=1
∴方程组的解为:$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$
(2)$\left\{\begin{array}{l}{2x+3y=7①}\\{3x+y=7②}\end{array}\right.$
②×3得:9x+3y=21③
③-①得,7x=14
x=2
将x=2代入②得,6+y=7
y=1
∴方程组的解为$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$
点评 本题考查二元一次方程组的解法,解题的关键是熟练运用二元一次方程组的解法,本题属于基础题型.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
14.把直线y=2x-1向左平移1个单位,平移后直线的关系式为( )
| A. | y=2x-2 | B. | y=2x+1 | C. | y=2x | D. | y=2x+2 |
16. 如图,在矩形ABCD中,AB=3,∠AOB=60°,则OC的长为( )
如图,在矩形ABCD中,AB=3,∠AOB=60°,则OC的长为( )
 如图,在矩形ABCD中,AB=3,∠AOB=60°,则OC的长为( )
如图,在矩形ABCD中,AB=3,∠AOB=60°,则OC的长为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
13.正如我们小学学过的圆锥体积公式V=$\frac{1}{3}$πr2h(π表示圆周率,r表示圆锥的底面半径,h表示圆锥的高)一样,许多几何量的计算都要用到π.祖冲之是世界上第一个把π计算到小数点后7位的中国古代科学家,创造了当时世界上的最高水平,差不多过了1000年,才有人把π计算得更精确.在辉煌成就的背后,我们来看看祖冲之付出了多少.现在的研究表明,仅仅就计算来讲,他至少要对9位数字反复进行130次以上的各种运算,包括开方在内.即使今天我们用纸笔来算,也绝不是一件轻松的事情,何况那时候没有现在的纸笔,数学计算不是用现在的阿拉伯数字,而是用算筹(小竹棍或小竹片)进行的,这需要怎样的细心和毅力啊!他这种严谨治学的态度,不怕复杂计算的毅力,值得我们学习.
下面我们就来通过计算解决问题:已知圆锥的侧面展开图是个半圆,若该圆锥的体积等于9$\sqrt{3}$π,则这个圆锥的高等于( )
下面我们就来通过计算解决问题:已知圆锥的侧面展开图是个半圆,若该圆锥的体积等于9$\sqrt{3}$π,则这个圆锥的高等于( )
| A. | $5\sqrt{3}π$ | B. | $5\sqrt{3}$ | C. | $3\sqrt{3}π$ | D. | $3\sqrt{3}$ |
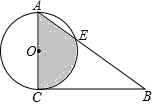 如图,在△ABC中,∠ACB=90°,AC=2,∠B=30°,以AC为直径作圆交AB于点E,则图中阴影部分的面积为$\frac{1}{3}$π+$\frac{\sqrt{3}}{4}$.
如图,在△ABC中,∠ACB=90°,AC=2,∠B=30°,以AC为直径作圆交AB于点E,则图中阴影部分的面积为$\frac{1}{3}$π+$\frac{\sqrt{3}}{4}$.