题目内容
15.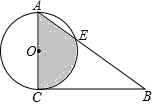 如图,在△ABC中,∠ACB=90°,AC=2,∠B=30°,以AC为直径作圆交AB于点E,则图中阴影部分的面积为$\frac{1}{3}$π+$\frac{\sqrt{3}}{4}$.
如图,在△ABC中,∠ACB=90°,AC=2,∠B=30°,以AC为直径作圆交AB于点E,则图中阴影部分的面积为$\frac{1}{3}$π+$\frac{\sqrt{3}}{4}$.
分析 连接OE,过点O作OF⊥AE,垂直为E,可证明△OAE为等边三角形,阴影部分的面积等于半圆的面积减去弓形面积.
解答 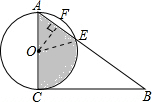 解:连接OE,过点O作OF⊥AE,垂直为E,
解:连接OE,过点O作OF⊥AE,垂直为E,
∵∠ACB=90°,AC=2,∠B=30°,
∴∠A=60°,
∴OA=1,
∴OF=$\frac{\sqrt{3}}{2}$,
∴S阴影=S半圆-S弓形
=S半圆-S扇形AOE+S扇形AOE
=$\frac{1}{2}$π-$\frac{60π•{1}^{2}}{360}$+$\frac{1}{2}$×1×$\frac{\sqrt{3}}{2}$=$\frac{1}{3}$π+$\frac{\sqrt{3}}{4}$.
点评 本题考查了扇形的面积公式,掌握扇形的面积公式是解题的关键.

练习册系列答案
相关题目
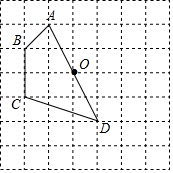 如图,正方形网格中的每一个小正方形的边长都是1,四边形ABCD的四个顶点都在格点上,O为AD边的中点,若把四边形ABCD绕着点O顺时针旋转90°,试解决下列问题:
如图,正方形网格中的每一个小正方形的边长都是1,四边形ABCD的四个顶点都在格点上,O为AD边的中点,若把四边形ABCD绕着点O顺时针旋转90°,试解决下列问题: 请从以下两个小题中任选一个作答,若多选,则按第一题计分.
请从以下两个小题中任选一个作答,若多选,则按第一题计分.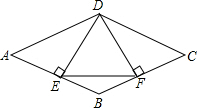 如图,在菱形ABCD中,过点D作DE⊥AB于点E,作DF⊥BC于点F,连接EF.
如图,在菱形ABCD中,过点D作DE⊥AB于点E,作DF⊥BC于点F,连接EF.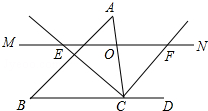 如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC,设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC,设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.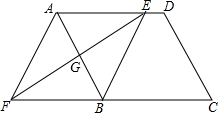 如图,在平行四边形ABCD中,边AB的垂直平分线交AD于点E,交CB的延长线于点F,连接AF,BE.
如图,在平行四边形ABCD中,边AB的垂直平分线交AD于点E,交CB的延长线于点F,连接AF,BE.