题目内容
14.已知等边△ABC的边长为12,D是AB上的动点,过D作DE⊥AC于点E,过E作EF⊥BC于点F,过F作FG⊥AB于点G.当G与D重合时,AD的长是( )| A. | 3 | B. | 4 | C. | 8 | D. | 9 |
分析 设BD=x,根据等边三角形的性质得到∠A=∠B=∠C=60°,由垂直的定义得到∠BDF=∠DEA=∠EFC=90°,解直角三角形即可得到结论.
解答 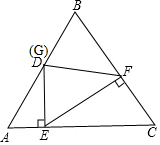 解:如图,设BD=x,
解:如图,设BD=x,
∵△ABC是等边三角形,
∴∠A=∠B=∠C=60°,
∵DE⊥AC于点E,EF⊥BC于点F,FG⊥AB,
∴∠BDF=∠DEA=∠EFC=90°,
∴BF=2x,
∴CF=12-2x,
∴CE=2CF=24-4x,
∴AE=12-CE=4x-12,
∴AD=2AE=8x-24,
∵AD+BD=AB,
∴8x-24+x=12,
∴x=4,
∴AD=8x-24=32-24=8.
故选C.
点评 本题考查了等边三角形的性质,含30°角的直角三角形的性质,熟练掌握等边三角形的性质是解题的关键.

练习册系列答案
相关题目
19.志远要在报纸上刊登广告,一块10cm×5cm的长方形版面要付广告费180元,他要把该版面的边长都扩大为原来的3倍,在每平方厘米版面广告费相同的情况下,他该付广告费( )
| A. | 540元 | B. | 1080元 | C. | 1620元 | D. | 1800元 |
11.下列各式变形正确的是( )
| A. | $\frac{2}{2+a}$=$\frac{1}{1+a}$ | B. | $\frac{a+1}{{a}^{2}+1}$=$\frac{1}{a+1}$ | C. | $\frac{-x+y}{x-y}$=$\frac{x+y}{y-x}$ | D. | $\frac{{a}^{2}-1}{a+1}$=a-1 |
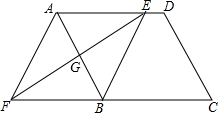 如图,在平行四边形ABCD中,边AB的垂直平分线交AD于点E,交CB的延长线于点F,连接AF,BE.
如图,在平行四边形ABCD中,边AB的垂直平分线交AD于点E,交CB的延长线于点F,连接AF,BE.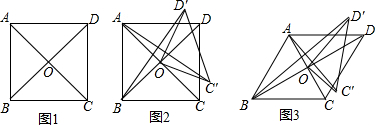
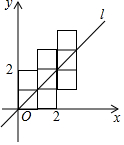 如图,将八个边长为1的小正方形摆放在平面直角坐标系中,若过原点的直线l将图形分成面积相等的两部分,则将直线l向右平移3个单位后所得直线l′的函数关系式为y=$\frac{10}{9}$x-$\frac{10}{3}$.
如图,将八个边长为1的小正方形摆放在平面直角坐标系中,若过原点的直线l将图形分成面积相等的两部分,则将直线l向右平移3个单位后所得直线l′的函数关系式为y=$\frac{10}{9}$x-$\frac{10}{3}$.