题目内容
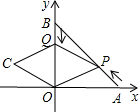 如图,A、B两点的坐标分别为(6,0)、(0,6),连结AB.点P从点A出发,沿AB方向以每秒
如图,A、B两点的坐标分别为(6,0)、(0,6),连结AB.点P从点A出发,沿AB方向以每秒| 2 |
考点:翻折变换(折叠问题),坐标与图形性质,平行四边形的性质
专题:动点型
分析:连接PC,过点P作PD⊥x轴于D,根据翻折变换的性质可得PC⊥OB,设运动时间为t秒时四边形QPOC为平行四边形,根据点A、B的坐标求出OA=OB,然后判断出△AOB是等腰直角三角形,再判断出△APD是等腰直角三角形,根据等腰直角三角形的性质求出PD,再求出OQ,然后根据OQ=2PD列式方程求出t的值,再求出点P的坐标,再根据轴对称性写出点C的坐标即可.
解答: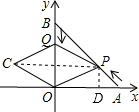 解:连接PC,过点P作PD⊥x轴于D,
解:连接PC,过点P作PD⊥x轴于D,
∵△PQO沿BO翻折点P的对应点为点C,
∴PC⊥OB,
设t秒时四边形QPOC为平行四边形,
则AP=
t,BQ=t,
∵A(6,0),B(0,6),
∴OA=OB=6,
∴△AOB是等腰直角三角形,△APD是等腰直角三角形,
∴PD=
AP=
×
t=t,
∵四边形QPOC为平行四边形,
∴OQ=2PD,
∴6-t=2t,
解得t=2,
∴AD=PD=2,
OD=OA-AD=6-2=4,
∴点P的坐标为(4,2),
∵点P、C关于OB对称,
∴点C的坐标为(-4,2).
故答案为:(-4,2).
 解:连接PC,过点P作PD⊥x轴于D,
解:连接PC,过点P作PD⊥x轴于D,∵△PQO沿BO翻折点P的对应点为点C,
∴PC⊥OB,
设t秒时四边形QPOC为平行四边形,
则AP=
| 2 |
∵A(6,0),B(0,6),
∴OA=OB=6,
∴△AOB是等腰直角三角形,△APD是等腰直角三角形,
∴PD=
| ||
| 2 |
| ||
| 2 |
| 2 |
∵四边形QPOC为平行四边形,
∴OQ=2PD,
∴6-t=2t,
解得t=2,
∴AD=PD=2,
OD=OA-AD=6-2=4,
∴点P的坐标为(4,2),
∵点P、C关于OB对称,
∴点C的坐标为(-4,2).
故答案为:(-4,2).
点评:本题考查了翻折变换的性质,坐标与图形性质,平行四边形的对角线互相平分的性质,熟记各性质并判断出OQ=2PD并列出方程是解题的关键.

练习册系列答案
相关题目
将4x2+1加上一个单项式所得的和为完全平方式,则这个单项式不可能是( )
| A、-4x4 |
| B、-4x |
| C、4x |
| D、4x4 |
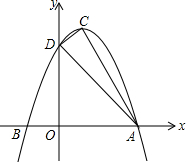 如图,抛物线y=ax2+bx+c的顶点为C(1,4),交x轴于点A(3,0),交y轴于点D.
如图,抛物线y=ax2+bx+c的顶点为C(1,4),交x轴于点A(3,0),交y轴于点D. 如图,已知点O是四边形ABCD内一点,且有OA=OB=OC,∠ABC=70°,则∠AOC=
如图,已知点O是四边形ABCD内一点,且有OA=OB=OC,∠ABC=70°,则∠AOC=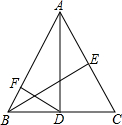 如图△ABC是等边三角形,AD是高,BE是角平分线,DF⊥AB于点F.若DF=1,则BE的长为
如图△ABC是等边三角形,AD是高,BE是角平分线,DF⊥AB于点F.若DF=1,则BE的长为 如图,正方形ABCD中,对角线AC与BD相交于点O,DE平分∠CDB交BC于E,交AC于F,则BC:OF=
如图,正方形ABCD中,对角线AC与BD相交于点O,DE平分∠CDB交BC于E,交AC于F,则BC:OF= 如图,在锐角△ABC中,AC=7cm,S△ABC=14cm2,AD平分∠BAC,M、N分别是AD和AB上的动点,则BM+MN的最小值是
如图,在锐角△ABC中,AC=7cm,S△ABC=14cm2,AD平分∠BAC,M、N分别是AD和AB上的动点,则BM+MN的最小值是