题目内容
 如图,正方形ABCD中,对角线AC与BD相交于点O,DE平分∠CDB交BC于E,交AC于F,则BC:OF=
如图,正方形ABCD中,对角线AC与BD相交于点O,DE平分∠CDB交BC于E,交AC于F,则BC:OF=考点:正方形的性质,角平分线的性质
专题:
分析:根据正方形的对角线平分一组对角线可得∠BDC=45°,根据角平分线的定义可得∠BDE=∠CDE=22.5°,再根据直角三角形两锐角互余求出∠OFD=∠CED=67.5°,根据对顶角相等可得∠OFD=∠CFE,从而得到∠CED=∠CFE,根据等角对等边可得CE=CF,设正方形的边长为2x,根据正方形的性质求出OC=OD=
x,再用OF表示出CF,即CE,然后利用△ODF和△CDE相似,根据相似三角形对应边成比例列式求出OF,然后求出比值即可.
| 2 |
解答:解:在正方形ABCD中,∠BDC=45°,
∵DE平分∠CDB,
∴∠BDE=∠CDE=
×45°=22.5°,
∴∠OFD=∠CED=90°-22.5°=67.5°,
∵∠OFD=∠CFE(对顶角相等),
∴∠CED=∠CFE,
∴CE=CF,
设正方形的边长为2x,
则OC=OD=
×2x=
x,
∴CF=
x-OF,
∵∠BDE=∠CDE,∠DOF=∠DCE=90°,
∴△ODF∽△CDE,
∴
=
,
即
=
,
解得OF=(2-
)x,
∴BC:OF=2x:(2-
)x=2+
.
故答案为:2+
.
∵DE平分∠CDB,
∴∠BDE=∠CDE=
| 1 |
| 2 |
∴∠OFD=∠CED=90°-22.5°=67.5°,
∵∠OFD=∠CFE(对顶角相等),
∴∠CED=∠CFE,
∴CE=CF,
设正方形的边长为2x,
则OC=OD=
| ||
| 2 |
| 2 |
∴CF=
| 2 |
∵∠BDE=∠CDE,∠DOF=∠DCE=90°,
∴△ODF∽△CDE,
∴
| OF |
| CE |
| OD |
| CD |
即
| OF | ||
|
| ||
| 2x |
解得OF=(2-
| 2 |
∴BC:OF=2x:(2-
| 2 |
| 2 |
故答案为:2+
| 2 |
点评:本题考查了正方形的性质,角平分线的定义,相似三角形的判定与性质,熟记各性质是解题的关键,设出正方形的边长并表示出OF是本题的难点.

练习册系列答案
相关题目
如图,y是x的函数图象的是( )
A、 |
B、 |
C、 |
D、 |
下列各式中,运算正确的是( )
| A、2a+3b=5ab |
| B、a2b-ab2=0 |
| C、(2ab)2=4a2b2 |
| D、(a+b)2=a2+b2 |
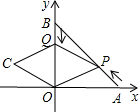 如图,A、B两点的坐标分别为(6,0)、(0,6),连结AB.点P从点A出发,沿AB方向以每秒
如图,A、B两点的坐标分别为(6,0)、(0,6),连结AB.点P从点A出发,沿AB方向以每秒