题目内容
 如图,在锐角△ABC中,AC=7cm,S△ABC=14cm2,AD平分∠BAC,M、N分别是AD和AB上的动点,则BM+MN的最小值是
如图,在锐角△ABC中,AC=7cm,S△ABC=14cm2,AD平分∠BAC,M、N分别是AD和AB上的动点,则BM+MN的最小值是考点:轴对称-最短路线问题
专题:
分析:根据题意画出符合条件的图形,作N关于AD的对称点为R,作AC边上的高BE(E在AC上),求出BM+MN=BR,根据垂线段最短得出BM+MN≥BE,求出BE即可得出BM+MN的最小值.
解答:解:作N关于AD的对称点为R,作AC边上的高BE(E在AC上),
∵AD平分∠CAB,△ABC为锐角三角形,
∴R必在AC上,
∵N关于AD的对称点为R,
∴MR=MN,
∴BM+MN=BM+MR,
即BM+MN=BR≥BE(垂线段最短),
∵△ABC的面积是14cm2,AC=7,
∴
×7×BE=14,
∴BE=4,
即BM+MN的最小值为4cm.
故答案为:4.

∵AD平分∠CAB,△ABC为锐角三角形,
∴R必在AC上,
∵N关于AD的对称点为R,
∴MR=MN,
∴BM+MN=BM+MR,
即BM+MN=BR≥BE(垂线段最短),
∵△ABC的面积是14cm2,AC=7,
∴
| 1 |
| 2 |
∴BE=4,
即BM+MN的最小值为4cm.
故答案为:4.
点评:本题考查了平面展开-最短路线问题,关键是画出符合条件的图形,题目具有一定的代表性,是一道比较好的题目.

练习册系列答案
相关题目
已知a,b,c是三角形的三边长,如果满足(a-b)2+
+|c2-64|=0,则三角形的形状是( )
| b-8 |
| A、底和腰不相等的等腰三角形 |
| B、等边三角形 |
| C、钝角三角形 |
| D、直角三角形 |
如图,y是x的函数图象的是( )
A、 |
B、 |
C、 |
D、 |
下列各数组中,能作为直角三角形三边长的是( )
| A、1,1,2 |
| B、2,3,4 |
| C、2,3,5 |
| D、3,4,5 |
如果a2+8ab+m是一个完全平方式,则m可以是( )
| A、b2 |
| B、2b |
| C、4b |
| D、16b2 |
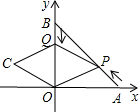 如图,A、B两点的坐标分别为(6,0)、(0,6),连结AB.点P从点A出发,沿AB方向以每秒
如图,A、B两点的坐标分别为(6,0)、(0,6),连结AB.点P从点A出发,沿AB方向以每秒