题目内容
17.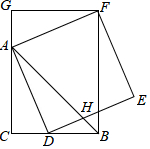 如图,在△ABC中,∠ACB=90°,AC=BC,AD平分∠BAC交BC于点D,以AD为边作正方形ADEF,过点F作FG⊥CA交CA的延长线于点G,连接FB交DE于点H,下列结论:
如图,在△ABC中,∠ACB=90°,AC=BC,AD平分∠BAC交BC于点D,以AD为边作正方形ADEF,过点F作FG⊥CA交CA的延长线于点G,连接FB交DE于点H,下列结论:①∠BAF=∠GAF;
②四边形CBFG是矩形;
③AB=FH;
④AF2=FH•BC
其中正确的结论有①②④(把所有正确结论的序号都写在横线上)
分析 由△AFG≌△DAC,推出四边形BCGF是矩形,推出△BAF是等腰三角形,推出△AFG∽△HFE,由此即可一一判断.
解答 解:∵四边形ABCD是正方形,
∴AD=AF,∠DAF=90°,
∴FG⊥CG,
∴∠G=∠C=90°,
∴∠CAD+∠GAF=90°,∠GAF+∠AFG=90°,
∴∠CAD=∠AFG,
∴△AFG≌△DAC,
∴FG=AC=BC,∠ADC=∠FAG,
∴∠G+∠C=180°,
∴FG∥BC,
∴四边形BCGF是平行四边形,
∵∠G=90°,
∴四边形BCGF是矩形,故②正确,
∴CG∥BF,
∴∠GAF=∠AFB,
∵∠DAH+∠BAF=90°,∠DAB=∠DAC,
∴∠BAF=∠GAF,
∴∠BAF=∠AFB,故①正确,
∴BA=BF,易知FH<BF,故③错误,
∵∠GFB=∠AFE=90°,
∴∠GFA=∠BFE,∵∠G=∠E=90°,
∴△GFA≌△EFH,
∴$\frac{FA}{FH}$=$\frac{GF}{EF}$,
∵EF=AF,GF=AC,
∴AF2=FH•AC.
故答案为①②④.
点评 本题考查正方形的性质、矩形的判定和性质、全等三角形的判定和性质,相似三角形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
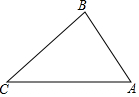 如图,在△ABC中,∠C=45°,∠B=75°,BC=$\sqrt{6}$,求AB的长.
如图,在△ABC中,∠C=45°,∠B=75°,BC=$\sqrt{6}$,求AB的长.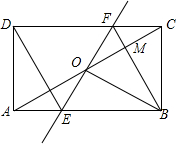 如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB、CD交于点E、F,连结BF交AC于点M,连结DE、BO.若∠COB=60°,FO=FC,则下列结论:①FB垂直平分OC;②△EOB≌△CMB;③DE=EF;④S△AOE:S△BCM=2:3.其中一定成立的结论有①③④(将正确结论的序号填在横线上)
如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB、CD交于点E、F,连结BF交AC于点M,连结DE、BO.若∠COB=60°,FO=FC,则下列结论:①FB垂直平分OC;②△EOB≌△CMB;③DE=EF;④S△AOE:S△BCM=2:3.其中一定成立的结论有①③④(将正确结论的序号填在横线上) 如图,A、B两点被池塘隔开,请你运用所学知识,说说怎样测出A、B两点间的距离?根据是什么?
如图,A、B两点被池塘隔开,请你运用所学知识,说说怎样测出A、B两点间的距离?根据是什么?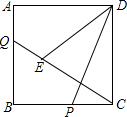 如图,四边形ABCD为正方形,AD=3,点P、点Q分别是BC、AB边上的动点,CP=AQ,连接DP、CQ,在线段CQ上有一动点E,满足∠DEC=∠DPC,则CE•CQ的值为9.
如图,四边形ABCD为正方形,AD=3,点P、点Q分别是BC、AB边上的动点,CP=AQ,连接DP、CQ,在线段CQ上有一动点E,满足∠DEC=∠DPC,则CE•CQ的值为9.