��Ŀ����
7�� ��ͼ����Rt��ABC�У���C=90�㡢AC=BC=4����P�ӵ�C������CA��ÿ��1����λ���ȵ��ٶ����յ�A�˶���ͬʱ����Q�ӵ�C������CB-BA�˶�����Q��CB�ϵ��ٶ�Ϊÿ��2����λ���ȣ���BA�ϵ��ٶ�Ϊÿ��$\sqrt{2}$����λ���ȣ�����P����A��ʱ����Q��ֹ֮ͣ�˶�����CP��CQΪ�ڱ���?CPMQ����?CPMQ���ABC�ص�����ͼ�ε����Ϊy����P���˶�ʱ��Ϊx�룮
��ͼ����Rt��ABC�У���C=90�㡢AC=BC=4����P�ӵ�C������CA��ÿ��1����λ���ȵ��ٶ����յ�A�˶���ͬʱ����Q�ӵ�C������CB-BA�˶�����Q��CB�ϵ��ٶ�Ϊÿ��2����λ���ȣ���BA�ϵ��ٶ�Ϊÿ��$\sqrt{2}$����λ���ȣ�����P����A��ʱ����Q��ֹ֮ͣ�˶�����CP��CQΪ�ڱ���?CPMQ����?CPMQ���ABC�ص�����ͼ�ε����Ϊy����P���˶�ʱ��Ϊx�룮��1������M����AB��ʱ����x��ֵ��
��2������Q�ڱ�CB���˶�ʱ����y��x�ĺ�����ϵʽ
��3��ֱ��д����P��Q���������˶������У���?CPMQ���ABC�ص�����ͼ�β����ı���ʱ��x��ȡֵ��Χ��
���� ��1��ֻҪ֤���ı���CPMQ�Ǿ��Σ���MQB�ǵ���ֱ�������Σ��г����̼��ɽ�����⣮
��2���������������ۼ��ɢ���ͼ2�У��ٵ�0��t��$\frac{4}{3}$ʱ���ص��������ı���CPMQ���ڢ���ͼ3�У�$\frac{4}{3}$��t��2ʱ���ص������������CPEFQ���ֱ���㼴�ɣ�
��3������ͼ4��ͼ5����ϣ�2����ͼ�Σ������жϣ�
��� �⣺��1����ͼ1�У�
�ߡ�C=90�㡢AC=BC=4���ı���CPMQ��ƽ���ı��Σ�
���ı���CPMQ�Ǿ��Σ���A=��B=45�㣬
��AB��MQ��
���MQB=��C=90�㣬
���QMB=��B=45�㣬
��PC=MQ=BQ��
��2t+t=4��
��t=$\frac{4}{3}$��
��2����ͼ2�У��ٵ�0��t��$\frac{4}{3}$ʱ���ص��������ı���CPMQ��
y=t•2t=2t2��
����ͼ3�У�$\frac{4}{3}$��t��2ʱ���ص������������CPEFQ��
y=S�ı���CPMQ-S��EFM=2t2-$\frac{1}{2}$��3t-4��2=-$\frac{5}{2}$t2+12t-8��
��������y=$\left\{\begin{array}{l}{2{t}^{2}}&{��0��t��\frac{4}{3}��}\\{-\frac{5}{2}{t}^{2}+12t-8}&{��\frac{4}{3}��t��2��}\end{array}\right.$��
��3����ͼ4�У���Q��B�غ�ʱ���ص��������ı��Σ�
��ͼ5�У�����P��A�غ�ʱ���ص������������Σ�
����P��Q���������˶������У���?CPMQ���ABC�ص�����ͼ�β����ı���ʱ��x��ȡֵ��ΧΪ$\frac{4}{3}$��t��2��t=4��
���� ���⿼���ı����ۺ��⡢ƽ���ı��ε����ʡ����ε��ж������ʵ�֪ʶ������Ĺؼ���ѧ��������ۣ���Ҫ��ȷ����ͼ�Σ������п��������ͣ�

 ��ʦ�㲦��ϵ�д�
��ʦ�㲦��ϵ�д�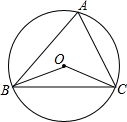 ��ͼ��ԲO�ǡ�ABC�����Բ����A=68�㣬���BOC�Ĵ�С�ǣ�������
��ͼ��ԲO�ǡ�ABC�����Բ����A=68�㣬���BOC�Ĵ�С�ǣ�������| A�� | 22�� | B�� | 32�� | C�� | 136�� | D�� | 68�� |
 ��ͼ����P��m��1���Ƿ���������y=$\frac{\sqrt{3}}{x}$ͼ���ϵ�һ�㣬PT��x���ڵ�T���ѡ�PTO
��ͼ����P��m��1���Ƿ���������y=$\frac{\sqrt{3}}{x}$ͼ���ϵ�һ�㣬PT��x���ڵ�T���ѡ�PTO ��֪���ı���ABCD�У�BDƽ�֡�ABC��AB=4��BC=9��BD6ʱ����ABD�ס�DBC��
��֪���ı���ABCD�У�BDƽ�֡�ABC��AB=4��BC=9��BD6ʱ����ABD�ס�DBC�� ��֪����AOB����M��N����������P��ʹ��P�ڡ�AOB��ƽ�����ϣ���PM=PN����Ҫ���ó߹���ͼ��������ͼ�ۼ�����д��������
��֪����AOB����M��N����������P��ʹ��P�ڡ�AOB��ƽ�����ϣ���PM=PN����Ҫ���ó߹���ͼ��������ͼ�ۼ�����д��������