题目内容
19.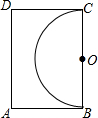 如图,王大伯家屋后有一块长12m,宽8m的矩形空地,他在以长边BC为直径的半圆内种菜,他家养的一只羊平时拴A处的一棵树上,为了不让羊吃到菜,拴羊的绳长可以选用( )
如图,王大伯家屋后有一块长12m,宽8m的矩形空地,他在以长边BC为直径的半圆内种菜,他家养的一只羊平时拴A处的一棵树上,为了不让羊吃到菜,拴羊的绳长可以选用( )| A. | 3m | B. | 5m | C. | 7m | D. | 9m |
分析 为了不让羊吃到菜,必须小于等于点A到圆的最小距离.要确定最小距离,连接OA交半圆于点E,即AE是最短距离.在直角三角形AOB中,因为OB=6,AB=8,所以根据勾股定理得OA=10.那么AE的长即可解答.
解答  解:连接OA,交半圆O于E点,
解:连接OA,交半圆O于E点,
在Rt△OAB中,OB=6cm,AB=8cm,
所以OA=$\sqrt{O{B}^{2}+A{B}^{2}}$=10cm;
又OE=OB=6cm,
所以AE=OA-OE=4cm.
因此选用的绳子应该不大于4m,
故选:A.
点评 此题考查了勾股定理的应用,确定点到半圆的最短距离是难点.熟练运用勾股定理.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
14.在Rt△ABC中,∠C=90°,若AC=5,BC=12,则AB的长为( )
| A. | 5 | B. | 12 | C. | 13 | D. | 15 |
8.在△ABC中,a,b,c分别是∠A,∠B,∠C的对边,如果a2+b2=c2,那么下列结论正确的是( )
| A. | csinA=a | B. | bcosB=c | C. | atanA=b | D. | ctanB=b |
9.有一块多边形草坪,在市政建设设计图纸上的面积为300cm2,其中一条边的长度为5cm,经测量,这条边的实际长度为15m,则这块草坪的实际面积是( )
| A. | 100m2 | B. | 270m2 | C. | 2 700m2 | D. | 90 000m2 |
 如图,已知AB∥CD,OA=2,AD=9,OB=5,DC=12,∠A=58°,∠AOB=72°,求AB,OC的长及∠C的度数.
如图,已知AB∥CD,OA=2,AD=9,OB=5,DC=12,∠A=58°,∠AOB=72°,求AB,OC的长及∠C的度数. 如图,以⊙O的直径BC为边作等边△ABC,AB,AC分别交⊙O于点D,E.求证:BD=DE=EC.
如图,以⊙O的直径BC为边作等边△ABC,AB,AC分别交⊙O于点D,E.求证:BD=DE=EC.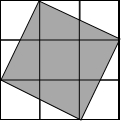 如图,在3×3的方格中,有一阴影正方形,设每一个小方格的边长为1个单位.请解决下面的问题.
如图,在3×3的方格中,有一阴影正方形,设每一个小方格的边长为1个单位.请解决下面的问题.