题目内容
9. 如图,已知AB∥CD,OA=2,AD=9,OB=5,DC=12,∠A=58°,∠AOB=72°,求AB,OC的长及∠C的度数.
如图,已知AB∥CD,OA=2,AD=9,OB=5,DC=12,∠A=58°,∠AOB=72°,求AB,OC的长及∠C的度数.
分析 先根据OA=2,AD=9求出OD的长,再根据△AOB∽△DOC即可得出$\frac{OA}{OD}$=$\frac{OB}{OC}$=$\frac{AB}{CD}$,再把已知数据代入进行计算即可.
解答 解:∵OA=2,AD=9,
∴OD=9-2=7,
∵AB∥CD,
∴△AOB∽△DOC,
∴$\frac{OA}{OD}=\frac{OB}{OC}=\frac{AB}{CD}$,
∵OA=2,OB=5,DC=12,
∴$\frac{2}{7}$=$\frac{5}{OC}$=$\frac{AB}{12}$,解得OC=$\frac{35}{2}$,AB=$\frac{24}{7}$,
∵△AOB∽△DOC,
∴∠D=∠A=58°,
∵∠COD=∠BOA=72°,
∴∠C=180°-58°-72°=50°.
点评 本题考查了相似三角形的性质和判定,三角形的内角和,对顶角相等,熟知相似三角形的对应边成比例是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.三元一次方程组$\left\{\begin{array}{l}{3x-2y=5}\\{x+y+z=2}\\{z=2}\end{array}\right.$的解是( )
| A. | $\left\{\begin{array}{l}{x=1}\\{y=1}\\{z=2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=1}\\{y=-1}\\{z=2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=-1}\\{y=1}\\{z=2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=-1}\\{y=-1}\\{z=2}\end{array}\right.$ |
14.△ABC的三边长分别为$\sqrt{2}$,$\sqrt{10}$和2,△A′B′C′的两边长分别为1和$\sqrt{5}$.如果△ABC∽△A′B′C′,则
△A′B′C′第三边的长为( )
△A′B′C′第三边的长为( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\sqrt{2}$ | C. | 2 | D. | 2$\sqrt{2}$ |
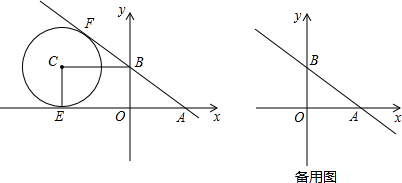
 如图,△ABC三定点在圆O上,AC是圆O的直径,∠C=52°,∠ABC平分线BD交圆O于点D,求∠BAD的度数.
如图,△ABC三定点在圆O上,AC是圆O的直径,∠C=52°,∠ABC平分线BD交圆O于点D,求∠BAD的度数. 如图,若△ABC∽△AED,AD=10cm,BD=12cm,AC=12cm,则AE=$\frac{55}{3}$cm.
如图,若△ABC∽△AED,AD=10cm,BD=12cm,AC=12cm,则AE=$\frac{55}{3}$cm.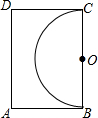 如图,王大伯家屋后有一块长12m,宽8m的矩形空地,他在以长边BC为直径的半圆内种菜,他家养的一只羊平时拴A处的一棵树上,为了不让羊吃到菜,拴羊的绳长可以选用( )
如图,王大伯家屋后有一块长12m,宽8m的矩形空地,他在以长边BC为直径的半圆内种菜,他家养的一只羊平时拴A处的一棵树上,为了不让羊吃到菜,拴羊的绳长可以选用( )