题目内容
14. 如图,点D在∠AOB的平分线OC上,点E在OA上,ED∥OB,∠1=25°,则∠AED的度数为50°.
如图,点D在∠AOB的平分线OC上,点E在OA上,ED∥OB,∠1=25°,则∠AED的度数为50°.
分析 根据平行线的性质得到∠3=∠1,根据角平分线的定义得到∠1=∠2,等量代换得到∠2=∠3,由三角形的外角的性质即可得到结论.
解答  解:∵ED∥OB,
解:∵ED∥OB,
∴∠3=∠1,
∵点D在∠AOB的平分线OC上,
∴∠1=∠2,
∴∠2=∠3,
∴∠AED=∠2+∠3=50°,
故答案为:50.
点评 本题考查了平行线的性质,角平分线的定义,三角形外角的性质,熟练掌握平行线的性质是解题的关键.

练习册系列答案
相关题目
4.若函数y=x2-2x+b的图象与坐标轴有三个交点,则b的取值范围是( )
| A. | b<1且b≠0 | B. | b>1 | C. | 0<b<1 | D. | b<1 |
2.如图1,在矩形ABCD中,动点E从A出发,沿AB→BC方向运动,当点E到达点C时停止运动,过点E做FE⊥AE,交CD于F点,设点E运动路程为x,FC=y,如图2所表示的是y与x的函数关系的大致图象,当点E在BC上运动时,FC的最大长度是$\frac{2}{5}$,则矩形ABCD的面积是( )
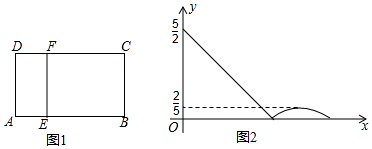

| A. | $\frac{23}{5}$ | B. | 5 | C. | 6 | D. | $\frac{25}{4}$ |
6.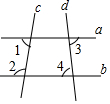 如图,直线a,b被直线c,d所截,若∠1=80°,∠2=100°,∠3=85°,则∠4度数是( )
如图,直线a,b被直线c,d所截,若∠1=80°,∠2=100°,∠3=85°,则∠4度数是( )
 如图,直线a,b被直线c,d所截,若∠1=80°,∠2=100°,∠3=85°,则∠4度数是( )
如图,直线a,b被直线c,d所截,若∠1=80°,∠2=100°,∠3=85°,则∠4度数是( )| A. | 80° | B. | 85° | C. | 95° | D. | 100° |
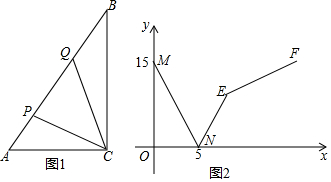
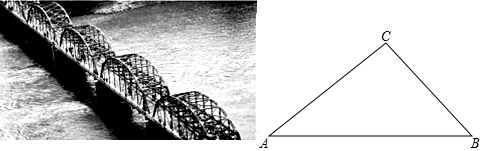
4.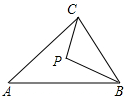 如图,在△ABC中,AB=AC,∠A=40°.如果P为三角形内一点,且∠PBC=∠PCA,那么∠BPC等于( )
如图,在△ABC中,AB=AC,∠A=40°.如果P为三角形内一点,且∠PBC=∠PCA,那么∠BPC等于( )
 如图,在△ABC中,AB=AC,∠A=40°.如果P为三角形内一点,且∠PBC=∠PCA,那么∠BPC等于( )
如图,在△ABC中,AB=AC,∠A=40°.如果P为三角形内一点,且∠PBC=∠PCA,那么∠BPC等于( )| A. | 110° | B. | 125° | C. | 130° | D. | 65° |
5.下列函数不是一次函数的是( )
| A. | y=-3x | B. | $y=\frac{2}{x}$ | C. | y=2x+8 | D. | y=1-x |