题目内容
 一次函数y=ax+6与y=cx-b的图象交于点P(1,b),一次函数y=ax+6的图象交y轴于点A,y=cx-b的图象交y轴于点B,如图所示.若△ABP的面积为4,则一次函数y=cx-b的图象与直线y=4和y轴所围成的阴影部分的面积为( )
一次函数y=ax+6与y=cx-b的图象交于点P(1,b),一次函数y=ax+6的图象交y轴于点A,y=cx-b的图象交y轴于点B,如图所示.若△ABP的面积为4,则一次函数y=cx-b的图象与直线y=4和y轴所围成的阴影部分的面积为( )| A、4 | B、4.5 | C、8 | D、9 |
考点:两条直线相交或平行问题
专题:
分析:根据△ABP的面积求得AB=8,进而求得OB=2,求得B(0,-2),从而求得b=2,对称P的坐标,进而求得直线y=cx-b的解析式,然后求得直线y=4x-2和直线y=4的交点坐标,即可求得阴影部分的面积.
解答:解:∵一次函数y=ax+6与y=cx-b的图象交于点P(1,b),△ABP的面积为4,
∴
AB×1=4,解得AB=8,
∵一次函数y=ax+6的图象交y轴于点A,
∴A(0,6),
∴OA=6,
∴OB=8-6=2,
∴B(0,-2),
∵一次函数y=cx-b的图象交y轴于点B,
∴b=2,
∴P(1,2),
∵一次函数y=cx-2的图象经过P,
∴2=c-2,解得c=4,
∴y=4x-2,
当y=4时,x=
,
∴阴影部分的面积=
(4+2)×
=9.
故选D.
∴
| 1 |
| 2 |
∵一次函数y=ax+6的图象交y轴于点A,
∴A(0,6),
∴OA=6,
∴OB=8-6=2,
∴B(0,-2),
∵一次函数y=cx-b的图象交y轴于点B,
∴b=2,
∴P(1,2),
∵一次函数y=cx-2的图象经过P,
∴2=c-2,解得c=4,
∴y=4x-2,
当y=4时,x=
| 3 |
| 2 |
∴阴影部分的面积=
| 1 |
| 2 |
| 3 |
| 2 |
故选D.
点评:本题考查了两条直线相交或平行的问题,交点坐标符合两条直线的解析式是关键,同时也考查了待定系数法求解析式.

练习册系列答案
相关题目
观察下列各式:0.
=
,0.
=
,0.
=
,又如0.
=
,0.52
=
,0.1
=
,0.35
=
,则把0.173
化成分数是( )
| • |
| 2 |
| 2 |
| 9 |
| •• |
| 23 |
| 23 |
| 99 |
| … |
| 153 |
| 153 |
| 999 |
| •• |
| 23 |
| 23-2 |
| 90 |
| • |
| 7 |
| 527-52 |
| 900 |
| •• |
| 26 |
| 126-1 |
| 990 |
| •• |
| 42 |
| 3542-35 |
| 9900 |
| •• |
| 29 |
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,BC=2,AC=
如图,BC=2,AC=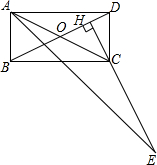 如图,在矩形ABCD中,点H在对角线BD上.HC⊥BD,HC的延长线交∠BAD的平分线于点E.求证:CE=BD.
如图,在矩形ABCD中,点H在对角线BD上.HC⊥BD,HC的延长线交∠BAD的平分线于点E.求证:CE=BD. 如图,学校位于高速路AB的一侧(AB成一直线),点A、点B为高速路上距学校直线距离最近的2个隧道出入口,点C、点D为学校的两幢教学楼.经测量,∠ACB=90°,∠ADB>90°,AC=600m,AB=1000m,D到高速路的最短直线距离DE=400m.
如图,学校位于高速路AB的一侧(AB成一直线),点A、点B为高速路上距学校直线距离最近的2个隧道出入口,点C、点D为学校的两幢教学楼.经测量,∠ACB=90°,∠ADB>90°,AC=600m,AB=1000m,D到高速路的最短直线距离DE=400m. 如图,在△ABC和△DEC中,∠BCE=∠ACD,BC=EC,请你添加一个条件,使得△ABC和△DEC全等.并加以证明.你添加的条件是
如图,在△ABC和△DEC中,∠BCE=∠ACD,BC=EC,请你添加一个条件,使得△ABC和△DEC全等.并加以证明.你添加的条件是 如图,OA⊥BC于点O,OD平分∠AOB,OE平分∠DOC,求∠DOE的度数.
如图,OA⊥BC于点O,OD平分∠AOB,OE平分∠DOC,求∠DOE的度数.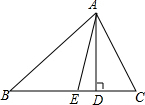 如图所示,在△ABC中,已知∠C>∠B,AD⊥BC于点D,AE平分∠BAC,判断∠EAD与
如图所示,在△ABC中,已知∠C>∠B,AD⊥BC于点D,AE平分∠BAC,判断∠EAD与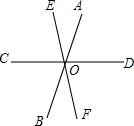 如图,直线AB,CD,EF相交于点O,∠AOE:∠AOD=1:3,∠COB:∠DOF=3:4,求证,CD⊥EF.
如图,直线AB,CD,EF相交于点O,∠AOE:∠AOD=1:3,∠COB:∠DOF=3:4,求证,CD⊥EF.