题目内容
 如图,等腰直角△ABC中,∠ACB=90°,点D、E在AB上,且∠DCE=45°,BE=2,AD=3.
如图,等腰直角△ABC中,∠ACB=90°,点D、E在AB上,且∠DCE=45°,BE=2,AD=3.(1)将△BCE绕点C逆时针旋转90°,画出旋转后的图形,并求DE的长;
(2)将△BCE沿直线CE翻折至△CEF,画出△CEF,并求DE的长.
考点:作图-旋转变换
专题:
分析:(1)将△CEB绕点C逆时针旋转90°,得到△ACF,连结DF,根据旋转的性质可得CE=CF,AF=BE,∠ACF=∠BCE,∠CAF=∠B=45°,然后求出∠DCF=45°,从而得到∠DCE=∠DCF,再利用“边角边”证明△CDE和△CDF全等,根据全等三角形对应边相等可得DF=DE,再求出△ADF是直角三角形,然后勾股定理得出DE2=AD2+BE2=32+22=13;
(2)根据轴对称的性质画出△CEF,由(1)可得DE的长.
(2)根据轴对称的性质画出△CEF,由(1)可得DE的长.
解答: 解:(1)如图,将△BCE绕点C逆时针旋转90°,得到△ACF,连结DF.
解:(1)如图,将△BCE绕点C逆时针旋转90°,得到△ACF,连结DF.
由旋转的性质得,CE=CF,AF=BE=2,∠ACF=∠BCE,∠CAF=∠B=45°,
∵∠ACB=90°,∠DCE=45°,
∴∠DCF=∠ACD+∠ACF=∠ACD+∠BCE=∠ACB-∠DCE=90°-45°=45°,
∴∠DCE=∠DCF,
在△CDE和△CDF中,
,
∴△CDE≌△CDF(SAS),
 ∴DF=DE,
∴DF=DE,
∵∠DAF=∠BAC+∠CAF=45°+45°=90°,
∴△ADF是直角三角形,
∴DF2=AD2+AF2,
∴DE2=AD2+BE2=32+22=13,
∴DE=
;
(2)如图所示,△CEF即为△BCE沿直线CE翻折后的图形,
由(1)可知DE=
.
 解:(1)如图,将△BCE绕点C逆时针旋转90°,得到△ACF,连结DF.
解:(1)如图,将△BCE绕点C逆时针旋转90°,得到△ACF,连结DF.由旋转的性质得,CE=CF,AF=BE=2,∠ACF=∠BCE,∠CAF=∠B=45°,
∵∠ACB=90°,∠DCE=45°,
∴∠DCF=∠ACD+∠ACF=∠ACD+∠BCE=∠ACB-∠DCE=90°-45°=45°,
∴∠DCE=∠DCF,
在△CDE和△CDF中,
|
∴△CDE≌△CDF(SAS),
 ∴DF=DE,
∴DF=DE,∵∠DAF=∠BAC+∠CAF=45°+45°=90°,
∴△ADF是直角三角形,
∴DF2=AD2+AF2,
∴DE2=AD2+BE2=32+22=13,
∴DE=
| 13 |
(2)如图所示,△CEF即为△BCE沿直线CE翻折后的图形,
由(1)可知DE=
| 13 |
点评:本题考查了作图-旋转变换,作图-翻折变换,旋转的性质,全等三角形的判定与性质,等腰直角三角形的性质,勾股定理,难度适中.准确作出旋转后的图形是解题的关键.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
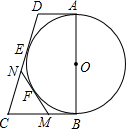 如图,四边形ABCD中,AD平行BC,∠ABC=90°,AD=2,AB=6,以AB为直径的半⊙O 切CD于点E,F为弧BE上一动点,过F点的直线MN为半⊙O的切线,MN交BC于M,交CD于N,则△MCN的周长为( )
如图,四边形ABCD中,AD平行BC,∠ABC=90°,AD=2,AB=6,以AB为直径的半⊙O 切CD于点E,F为弧BE上一动点,过F点的直线MN为半⊙O的切线,MN交BC于M,交CD于N,则△MCN的周长为( )| A、9 | ||
| B、10 | ||
C、3
| ||
D、2
|
下列四组线段中,可以构成直角三角形的是( )
| A、1.5,2,2.5 | ||
| B、4,5,6 | ||
| C、2,3,4 | ||
D、1,
|
下列调查中,不适合用普查的是( )
| A、旅客上飞机前的安检 |
| B、学校招聘教师,对应聘人员的面试 |
| C、了解一批灯泡的使用寿命 |
| D、了解全校学生的课外读书时间 |

 某校招生宣传栏中公布了担任七年级班主任的12位老师的情况如下表,小凤准备到该校就读七年级,请根据表中信息帮小凤进行如下统计分析:
某校招生宣传栏中公布了担任七年级班主任的12位老师的情况如下表,小凤准备到该校就读七年级,请根据表中信息帮小凤进行如下统计分析: 如图是某几何体的三视图.
如图是某几何体的三视图.