题目内容
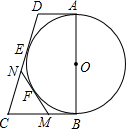 如图,四边形ABCD中,AD平行BC,∠ABC=90°,AD=2,AB=6,以AB为直径的半⊙O 切CD于点E,F为弧BE上一动点,过F点的直线MN为半⊙O的切线,MN交BC于M,交CD于N,则△MCN的周长为( )
如图,四边形ABCD中,AD平行BC,∠ABC=90°,AD=2,AB=6,以AB为直径的半⊙O 切CD于点E,F为弧BE上一动点,过F点的直线MN为半⊙O的切线,MN交BC于M,交CD于N,则△MCN的周长为( )| A、9 | ||
| B、10 | ||
C、3
| ||
D、2
|
考点:切线长定理
专题:计算题
分析:作DH⊥BC于H,如图,利用平行线的性质得AB⊥AD,AB⊥BC,则根据切线的判定得到AD和BC为⊙O切线,根据切线长定理得DE=DA=2,CE=CB,NE=NF,MB=MF,利用四边形ABHD为矩形得BH=AD=2,DH=AB=6,设BC=x,则CH=x-2,CD=x+2,在Rt△DCH中根据勾股定理得(x-2)2+62=(x+2)2,解得x=
,即CB=CE=
,然后由等线段代换得到△MCN的周长=CE+CB=9.
| 9 |
| 2 |
| 9 |
| 2 |
解答: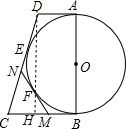 解:作DH⊥BC于H,如图,
解:作DH⊥BC于H,如图,
∵四边形ABCD中,AD平行BC,∠ABC=90°,
∴AB⊥AD,AB⊥BC,
∵AB为直径,
∴AD和BC为⊙O 切线,
∵CD和MN为⊙O 切线,
∴DE=DA=2,CE=CB,NE=NF,MB=MF,
∵四边形ABHD为矩形,
∴BH=AD=2,DH=AB=6,
设BC=x,则CH=x-2,CD=x+2,
在Rt△DCH中,∵CH2+DH2=DC2,
∴(x-2)2+62=(x+2)2,解得x=
,
∴CB=CE=
,
∴△MCN的周长=CN+CM+MN
=CN+CM+NF+MF
=CN+CM+NF+MB
=CE+CB
=9.
故选A.
 解:作DH⊥BC于H,如图,
解:作DH⊥BC于H,如图,∵四边形ABCD中,AD平行BC,∠ABC=90°,
∴AB⊥AD,AB⊥BC,
∵AB为直径,
∴AD和BC为⊙O 切线,
∵CD和MN为⊙O 切线,
∴DE=DA=2,CE=CB,NE=NF,MB=MF,
∵四边形ABHD为矩形,
∴BH=AD=2,DH=AB=6,
设BC=x,则CH=x-2,CD=x+2,
在Rt△DCH中,∵CH2+DH2=DC2,
∴(x-2)2+62=(x+2)2,解得x=
| 9 |
| 2 |
∴CB=CE=
| 9 |
| 2 |
∴△MCN的周长=CN+CM+MN
=CN+CM+NF+MF
=CN+CM+NF+MB
=CE+CB
=9.
故选A.
点评:本题考查了切线长定理:从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线,平分两条切线的夹角.也考查了勾股定理.

练习册系列答案
相关题目
下列事件属必然事件的是( )
| A、打开电视,正在直播NBA篮球赛 |
| B、早晨太阳一定从东方升起 |
| C、掷两次硬币,一定有一次正面朝上 |
| D、365人中一定有两人同一天出生 |
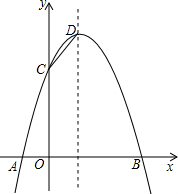 如图,已知抛物线与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C(0,3).
如图,已知抛物线与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C(0,3).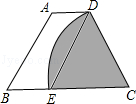 如图,等腰梯形ABCD中,AD∥BC,以点C为圆心,CD为半径的弧与BC交于点E,四边形ABED是平行四边形,AB=6,则扇形CDE(阴影部分)的面积是( )
如图,等腰梯形ABCD中,AD∥BC,以点C为圆心,CD为半径的弧与BC交于点E,四边形ABED是平行四边形,AB=6,则扇形CDE(阴影部分)的面积是( ) 如图,在平行四边形ABCD中,AB=6,AD=9,∠BAD的平行线交BC于E,交DC的延长线于F,BG垂直AE于G,BG=4
如图,在平行四边形ABCD中,AB=6,AD=9,∠BAD的平行线交BC于E,交DC的延长线于F,BG垂直AE于G,BG=4 如图,等腰直角△ABC中,∠ACB=90°,点D、E在AB上,且∠DCE=45°,BE=2,AD=3.
如图,等腰直角△ABC中,∠ACB=90°,点D、E在AB上,且∠DCE=45°,BE=2,AD=3. 为了测量某小球的直径,技术人员将小球放到透明烧杯上,如图是过球心O作为截面图,已知烧杯的高度是13cm,测得l=8cm,h=11cm,则小球的直径为
为了测量某小球的直径,技术人员将小球放到透明烧杯上,如图是过球心O作为截面图,已知烧杯的高度是13cm,测得l=8cm,h=11cm,则小球的直径为