题目内容
5.在理解例题的基础上,完成下列两个问题:例题:若m2+2mn+2n2-6n+9=0.求m和n的值.
解:因为m2+2mn+2n2-6n+9=(m2+2mn+n2)+(n2-6n+9)
=(m+n)2+(n-3)2=0
所以m+n=0,n-3=0
即m=-3.n=3
问题:
(1)若x2+2xy+2y2-4y+4=0,求xy的值.
(2)若a、b、c是△ABC的长,满足a2+b2=10a+8b-41,c是△ABC中最长边的边长,且c为整数,那么c可能是哪几个数?
分析 (1)已知等式变形后,利用完全平方公式变形,利用非负数的性质求出x与y的值,即可求出xy的值;
(2)由a2+b2=10a+8b-41,得a,b的值,然后利用三角形的三边关系求得c的取值范围即可.
解答 解:(1)∵x2+2xy+2y2-4y+4=0,
∴x2+2xy+y2+y2-4y+4=(x+y)2+(y-2)2=0,
∴x+y=0,y-2=0,
∴x=-y,y=2,
∴x=-2,y=2
则xy=-4.(2)
∵a2+b2=10a+8b-41,
∴a2+b2-8b-10a+41=0,
∴(a-4)2+(b-5)2=0,
∴a=4,b=5;
∴5-4<c<5+4,
∵c是最长边,c≤5,
∴5≤c<9,
∴c可能是5,6,7,8.
点评 此题考查了因式分解的应用,非负数的性质及三角形的三边关系,熟练掌握完全平方公式是解本题的关键

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.下列运算正确的是( )
| A. | a3•a2=a6 | B. | (-a3)2=a6 | C. | 2a+3a2=5a3 | D. | $3{a^3}÷2a=\frac{3}{2}{a^3}$ |
20. 通过计算几何图形的面积可表示一些代数恒等式,右图可表示的代数恒等式是( )
通过计算几何图形的面积可表示一些代数恒等式,右图可表示的代数恒等式是( )
 通过计算几何图形的面积可表示一些代数恒等式,右图可表示的代数恒等式是( )
通过计算几何图形的面积可表示一些代数恒等式,右图可表示的代数恒等式是( )| A. | (a-b)2=a2-2ab+b2 | B. | 2a(a+b)=2a2+2ab | C. | (a+b)2=a2+2ab+b2 | D. | (a+b)(a-b)=a2-b2 |
17.下列四个实数中,绝对值最大的数是( )
| A. | -$\sqrt{20}$ | B. | $\sqrt{15}$ | C. | $\root{3}{19}$ | D. | -$\root{3}{62}$ |
15.若a2-b2=$\frac{1}{4}$,a-b=$\frac{1}{2}$,则a+b的值为( )
| A. | -$\frac{1}{2}$ | B. | 1 | C. | $\frac{1}{2}$ | D. | 2 |
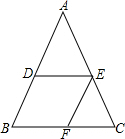 如图△ABC中,D、E分别是AB、AC中点,过E作EF∥AB交BC于F.
如图△ABC中,D、E分别是AB、AC中点,过E作EF∥AB交BC于F.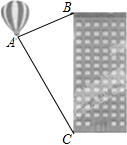 如图,据热气球的探测器显示,从热气球A看一栋高楼顶部B的仰角为30°,看这栋高楼底部C的俯角为60°,热气球A与高楼的水平距离为120m,求这栋高楼BC的高度.
如图,据热气球的探测器显示,从热气球A看一栋高楼顶部B的仰角为30°,看这栋高楼底部C的俯角为60°,热气球A与高楼的水平距离为120m,求这栋高楼BC的高度.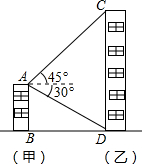 如图,甲楼AB的高度为21m,在甲楼楼顶A处测得乙楼顶端C处的仰角为45°,测得乙楼底部D处的俯角为30°.求乙楼CD的高度(结果精确到0.1米,$\sqrt{3}$≈1.73,$\sqrt{2}$,1.41)
如图,甲楼AB的高度为21m,在甲楼楼顶A处测得乙楼顶端C处的仰角为45°,测得乙楼底部D处的俯角为30°.求乙楼CD的高度(结果精确到0.1米,$\sqrt{3}$≈1.73,$\sqrt{2}$,1.41) 如图,直线AB、CD相交于点0,OE平分∠AOD,∠FOC=96°,∠BOF=40°,试求∠AOE的度数.
如图,直线AB、CD相交于点0,OE平分∠AOD,∠FOC=96°,∠BOF=40°,试求∠AOE的度数.