题目内容
15.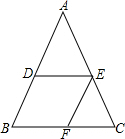 如图△ABC中,D、E分别是AB、AC中点,过E作EF∥AB交BC于F.
如图△ABC中,D、E分别是AB、AC中点,过E作EF∥AB交BC于F.(1)求证:四边形DBFE为平行四边形;
(2)当△ABC满足什么条件时,四边形DBFE为菱形,请说明理由.
分析 (1)根据三角形的中位线平行于第三边并且等于第三边的一半可得DE∥BC,然后根据两组对边分别平行的四边形是平行四边形证明;
(2)根据邻边相等的平行四边形是菱形,得出BD=BF,推出AB=BC即可.
解答 (1)证明:∵D、E分别是AB、AC的中点,
∴DE是△ABC的中位线,
∴DE∥BC,
又∵EF∥AB,
∴四边形DBFE是平行四边形;
(2)解:当AB=BC时,四边形DBFE是菱形.
理由如下:∵D是AB的中点,
∴BD=$\frac{1}{2}$AB,
∵DE是△ABC的中位线,
∴DE=$\frac{1}{2}$BC,
∵AB=BC,
∴BD=DE,
又∵四边形DBFE是平行四边形,
∴四边形DBFE是菱形.
点评 本题考查了三角形的中位线定理,平行四边形的判定,菱形的判定以及菱形与平行四边形的关系,熟记性质与判定方法是解题的关键.

练习册系列答案
相关题目
5.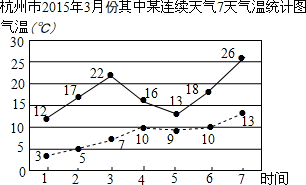 如图是2015年3月份其中某连续7天气温的统计图,其中实线表示最高气温,虚线表示最低气温,在下列结论中(某天中最高气温与最低气温的差值叫做温差):
如图是2015年3月份其中某连续7天气温的统计图,其中实线表示最高气温,虚线表示最低气温,在下列结论中(某天中最高气温与最低气温的差值叫做温差):
①这7天中温差最大的达13℃;
②这7天中各天最高气温与最低气温成正比关系;
③最高气温的中位数是17;
④该7天杭城气温变化较大.
你认为正确的是( )
 如图是2015年3月份其中某连续7天气温的统计图,其中实线表示最高气温,虚线表示最低气温,在下列结论中(某天中最高气温与最低气温的差值叫做温差):
如图是2015年3月份其中某连续7天气温的统计图,其中实线表示最高气温,虚线表示最低气温,在下列结论中(某天中最高气温与最低气温的差值叫做温差):①这7天中温差最大的达13℃;
②这7天中各天最高气温与最低气温成正比关系;
③最高气温的中位数是17;
④该7天杭城气温变化较大.
你认为正确的是( )
| A. | ①②③④ | B. | ①② | C. | ①③ | D. | ③④ |
10.函数y=$\sqrt{x+1}$自变量x的取值范围( )
| A. | x≥1 | B. | x≤-1 | C. | x≥-1 | D. | x≤1 |
4.虽然近几年无锡市政府加大了太湖水治污力度,但由于大规模、高强度的经济活动和日益增加的污染负荷,使部分太湖水域水质恶化,富营养化不断加剧.为了保护水资源,我市制定一套节水的管理措施,其中对居民生活用水收费作如下规定:
(1)若某用户六月份用水量为18吨,求其应缴纳的水费;
(2)记该用户六月份用水量为x吨,缴纳水费为y元,试列出y关于x的函数关系式;
(3)若该用户六月份用水量为40吨,缴纳水费y元的取值范围为70≤y≤90,试求m的取值范围.
| 月用水量(吨) | 单价(元/吨) |
| 不大于10吨部分 | 1.5 |
| 大于10吨不大于m吨部分(20≤m≤50) | 2 |
| 大于m吨部分 | 3 |
(2)记该用户六月份用水量为x吨,缴纳水费为y元,试列出y关于x的函数关系式;
(3)若该用户六月份用水量为40吨,缴纳水费y元的取值范围为70≤y≤90,试求m的取值范围.
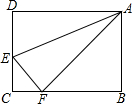 如图,在长方形ABCD中,AD=10cm,AB=8cm,E是CD上一点,若以AE为折痕,将△ADE翻折过来,顶点D恰与BC边上的点F复合,则△AEF的面积为25cm2.
如图,在长方形ABCD中,AD=10cm,AB=8cm,E是CD上一点,若以AE为折痕,将△ADE翻折过来,顶点D恰与BC边上的点F复合,则△AEF的面积为25cm2.