题目内容
20．
通过计算几何图形的面积可表示一些代数恒等式，右图可表示的代数恒等式是（ ）| A． | （a-b）2=a2-2ab+b2 | B． | 2a（a+b）=2a2+2ab | C． | （a+b）2=a2+2ab+b2 | D． | （a+b）（a-b）=a2-b2 |
分析 由题意知，长方形的面积等于长2a乘以宽（a+b），面积也等于四个小图形的面积之和，从而建立两种算法的等量关系．
解答 解：长方形的面积等于：2a（a+b），
也等于四个小图形的面积之和：a2+a2+ab+ab=2a2+2ab，
即2a（a+b）=2a2+2ab．
故选：B．
点评 本题考查了单项式乘多项式的几何解释，列出面积的两种不同表示方法是解题的关键．
练习册系列答案
相关题目
10．函数y=$\sqrt{x+1}$自变量x的取值范围（ ）
| A． | x≥1 | B． | x≤-1 | C． | x≥-1 | D． | x≤1 |
11．
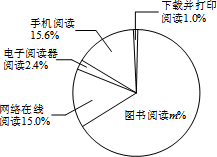宜兴市2010～2014年成年国民阅读调查报告的部分相关数据，绘制的统计图表如下：
根据以上信息解答下列问题：
（1）直接写出扇形统计图中m66的值；
（2）从2010到2014年，成年国民年人均阅读图书的数量每年增长的幅度近似相等，估算2015年成年国民年人均阅读图书的数量约为5本；
（3）2014年某小区倾向图书阅读的成年国民有990人，若该小区2015年与2014年成年国民的人数基本持平，估算2015年该小区成年国民阅读图书的总数量约为7500本．
宜兴市2010～2014年成年国民阅读调查报告的部分相关数据，绘制的统计图表如下：| 年份 | 年人均阅读图书数量（本） |
| 2010 | 3.90 |
| 2011 | 4.12 |
| 2012 | 4.35 |
| 2013 | 4.56 |
| 2014 | 4.78 |
（1）直接写出扇形统计图中m66的值；
（2）从2010到2014年，成年国民年人均阅读图书的数量每年增长的幅度近似相等，估算2015年成年国民年人均阅读图书的数量约为5本；
（3）2014年某小区倾向图书阅读的成年国民有990人，若该小区2015年与2014年成年国民的人数基本持平，估算2015年该小区成年国民阅读图书的总数量约为7500本．
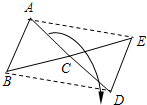已知：如图所示，△ABC为任意三角形，若将△ABC绕点C顺时针旋转180° 得到△DEC．
10．
如图，?ABCD中，∠ABC和∠BDC的平分线交AD边上一点E，且BE=4，CE=3，则BC的长是（ ）
如图，?ABCD中，∠ABC和∠BDC的平分线交AD边上一点E，且BE=4，CE=3，则BC的长是（ ）| A． | $\frac{5}{2}$ | B． | 3 | C． | 4 | D． | 5 |