题目内容
2.分式的乘除混合运算(1)$\frac{3a{b}^{2}}{2{x}^{3}y}$•(-$\frac{8xy}{9{a}^{2}b}$)÷$\frac{3x}{(-4b)}$
(2)$\frac{{y}^{2}-4y+4}{2y-6}$$•\frac{1}{y+3}$÷$\frac{12-6y}{9-{y}^{2}}$
(3)$\frac{(x-y)^{2}}{(y-x)^{3}}$•(x-y)4÷$\frac{9}{y-x}$
(4)(y-x)÷$\frac{{x}^{2}-2xy+{y}^{2}}{xy}$•$\frac{x-y}{{x}^{2}}$.
分析 (1)根据分式的乘除法进行计算,注意进行约分.
(2)根据分式的乘除法进行计算,注意进行约分.
(3)根据分式的乘除法进行计算,注意进行约分.
(4)根据分式的乘除法进行计算,注意进行约分.
解答 解:(1)原式=$\frac{3a{b}^{2}}{2{x}^{3}y}•(-\frac{8xy}{9{a}^{2}b})•\frac{-4b}{3x}$
=$\frac{16{b}^{2}}{9a{x}^{3}}$.
(2)原式=$\frac{(y-2)^{2}}{2(y-3)}•\frac{1}{y+3}•\frac{(3-y)(3+y)}{6(2-y)}$
=$\frac{y-2}{12}$.
(3)原式=$\frac{(x-y)^{2}}{(y-x)^{3}}•(x-y)^{4}•\frac{y-x}{9}$
=$\frac{(y-x)^{4}}{9}$.
(4)原式=$(y-x)•\frac{xy}{(x-y)^{2}}•\frac{x-y}{{x}^{2}}$
=-$\frac{y}{x}$.
点评 本题考查了分式的乘除法,解决本题的关键是遇到除法,变为乘法计算,并注意约分..

练习册系列答案
相关题目
17.a(x-y)与ay-ax的公因式是( )
| A. | a(x-y) | B. | ay+ax | C. | a | D. | x-y |
 如图,已知线段a,b,用直尺和圆规画图.
如图,已知线段a,b,用直尺和圆规画图.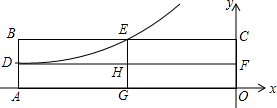 如图,矩形OABC的两边AB,BC分别与双曲线y=$\frac{k}{x}$(k<0)交于D,E两点,DF⊥y轴于F点,EG⊥x轴于G点,若矩形OGHF的面积为1,矩形OABC的面积为9,则k的值为-3.
如图,矩形OABC的两边AB,BC分别与双曲线y=$\frac{k}{x}$(k<0)交于D,E两点,DF⊥y轴于F点,EG⊥x轴于G点,若矩形OGHF的面积为1,矩形OABC的面积为9,则k的值为-3.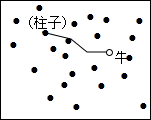 在一块空旷的草地上有一根拄子,柱子上拴着一条长5m的绳子,绳子的另一端拴着一头牛,如图所示.
在一块空旷的草地上有一根拄子,柱子上拴着一条长5m的绳子,绳子的另一端拴着一头牛,如图所示. 如图,在△ABC中,∠A=60°,∠B=45°,AC=8,CD⊥AB,垂足为点D,求AB的长.
如图,在△ABC中,∠A=60°,∠B=45°,AC=8,CD⊥AB,垂足为点D,求AB的长.