题目内容
12.已知直线y=-2x+4与x轴相交于点A,与y轴相交于点B.(1)求A、B两点的坐标;
(2)在下列坐标系作函数y=-2x+4的图象;
(3)求△AOB的面积;
(4)若点C(a+1,2a+2)在一次函数在直线y=-2x+4上,求C点的坐标;
(5)在x轴上是否存在点P使得△OCP是等腰三角形?若存在,直接写出P点的坐标;若不存在,请说明理由.
分析 (1)令y=0求出x的值,再令x=0求出y的值,即可得出A、B两点的坐标;
(2)根据A,B两点的坐标画出函数图象即可;
(3)根据三角形的面积公式即可得出结论;
(4)直接把点C(a+1,2a+2)代入一次函数y=-2x+4求出a的值,进而可得出C点坐标;
(5)先根据勾股定理求出OC的长,再分OC=OP,OC=PC,PC=OP三种情况进行讨论.
解答  解:(1)∵当y=0时,x=2;当x=0时,y=4,
解:(1)∵当y=0时,x=2;当x=0时,y=4,
∴A(2,0),B(0,4);
(2)如图所示;
(3)S△AOB=$\frac{1}{2}$×2×4=4;
(4)∵点C(a+1,2a+2)在一次函数在直线y=-2x+4上,
∴-2(a+1)+4=2a+2,解得a=0,
∵C(1,2);
(5)∵C(1,2),
∴OC=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$.
当OC=OP时,P1(-$\sqrt{5}$,0);
当OC=PC时,P2(2,0);
当PC=OP时,设P(x,0),则(x-1)2+22=x2,解得x=$\frac{5}{2}$,故P3($\frac{5}{2}$,0).
综上所示,P点坐标为P1(-$\sqrt{5}$,0),P2(2,0),P3($\frac{5}{2}$,0).
点评 本题考查的是一次函数综合题,涉及到一次函数图象上点的坐标特点,一次函数的性质等知识,在解答(3)时要注意进行分类讨论.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2. 已知数a,b,c在数轴上的位置如图所示,且|a|=|c|.化简:|a+c|-|5b|+|b-a|-|c-b|-|a+b|的结果是( )
已知数a,b,c在数轴上的位置如图所示,且|a|=|c|.化简:|a+c|-|5b|+|b-a|-|c-b|-|a+b|的结果是( )
 已知数a,b,c在数轴上的位置如图所示,且|a|=|c|.化简:|a+c|-|5b|+|b-a|-|c-b|-|a+b|的结果是( )
已知数a,b,c在数轴上的位置如图所示,且|a|=|c|.化简:|a+c|-|5b|+|b-a|-|c-b|-|a+b|的结果是( )| A. | -b-c | B. | 2b+c | C. | 2a-b+c | D. | -2a-b-c |
3.一个数的平方根与它的立方根相同,那么这个数是( )
| A. | 0 | B. | ±1 | C. | 1 | D. | 0和1 |
20.若|a|>0,下列叙述正确的是( )
| A. | a>0 | B. | a<0 | C. | a≠0 | D. | a=0 |
4.下列说法中,正确的是( )
| A. | 正整数、负整数统称为整数 | B. | 3.14不是有理数 | ||
| C. | 0是最小的有理数 | D. | 2.4是分数 |
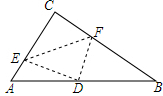 如图,在Rt△ABC中,∠C=90°,翻折∠C,使点C落在斜边AB上某一点D处,折痕为EF(点E,F分别在边AC,BC上).若△CEF与△ABC相似.
如图,在Rt△ABC中,∠C=90°,翻折∠C,使点C落在斜边AB上某一点D处,折痕为EF(点E,F分别在边AC,BC上).若△CEF与△ABC相似.