Question

10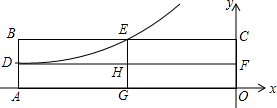．如图，矩形OABC的两边AB，BC分别与双曲线y=$\frac{k}{x}$（k＜0）交于D，E两点，DF⊥y轴于F点，EG⊥x轴于G点，若矩形OGHF的面积为1，矩形OABC的面积为9，则k的值为-3．

Answer 1

分析 设E（m，$\frac{k}{m}$），由矩形OGHF的面积为1得到OF=-$\frac{1}{m}$，于是根据反比例函数图象上点的坐标特征可表示出B点坐标为（km，$\frac{1}{m}$），接着利用矩形面积公式得到-km•$\frac{k}{m}$=9，然后解关于k的方程即可得到满足条件的k的值．

解答 解：设E（m，$\frac{k}{m}$），
∵矩形OGHF的面积为1，EG⊥x轴于G点，
∴OF=-$\frac{1}{m}$，
而DF⊥y轴于F点，
∴D点的纵坐标为-$\frac{1}{m}$，
当y=-$\frac{1}{m}$时，$\frac{k}{x}$=-$\frac{1}{m}$，解得x=-km，
∴D（-km，-$\frac{1}{m}$），
∴B（-km，$\frac{k}{m}$）
∵矩形OABC的面积为9，
∴km•$\frac{k}{m}$=9，
整理得k²=9，
而k＜0，
∴k=-3．
故答案为-3．

点评 本题考查了反比例函数比例系数k的几何意义：在反比例函数y=$\frac{k}{x}$图象中任取一点，过这一个点向x轴和y轴分别作垂线，与坐标轴围成的矩形的面积是定值|k|．