题目内容
3.如图,将1、$\sqrt{2}$、$\sqrt{3}$三个数按图中方式排列,若规定(a,b)表示第a排第b列的数,则
(1)(5,3)=1
(2)(8,2)与(2014,2014)表示的两个数的积是$\sqrt{3}$.
分析 (1)根据观察数列,可得,每三个数一循环,根据有序数对的表示方法,可得有序数对表示的数,确定出所求即可;
(2)根据(1)得出的规律计算即可得到答案.
解答 解:(1)每三个数一循环,1、$\sqrt{2}$、$\sqrt{3}$,则前4排共有1+2+3+4=10个数,
则(5,3)=1;
(2)每三个数一循环,1、$\sqrt{2}$、$\sqrt{3}$,则前7排共有1+2+3+4+5+6+7=28个数,
因此(8,2)在排列中是第28+2=30个,
30÷3=10,(8,2)表示的数正好是第10轮的最后一个,
即(8,2)表示的数是$\sqrt{3}$,
前2013排共有1+2+3…+2013=(1+2013)×2013÷2+2014=2029105个数,
2029105÷3=676368…1,
(2014,2014)表示的数正好是第676369轮的一个数,
即(2014,2014)表示的数是1,
则(8,2)与(2014,2014)表示的两个数的积是$\sqrt{3}$×1=$\sqrt{3}$,
故答案为:(1)1;(2)$\sqrt{3}$
点评 此题考查了数字的变化类,以及实数的运算,弄清题中的规律是解本题的关键.

练习册系列答案
 同步奥数系列答案
同步奥数系列答案
相关题目
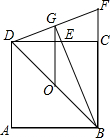 如图,O是正方形ABCD的中心,BE平分∠DBC,交DC于点E,将点E绕着点C按顺时针方向旋转90°得到点F,连接CF,DF,BE的延长线交DF于点G,连接OG.
如图,O是正方形ABCD的中心,BE平分∠DBC,交DC于点E,将点E绕着点C按顺时针方向旋转90°得到点F,连接CF,DF,BE的延长线交DF于点G,连接OG. 如图,将矩形ABCD沿对角线BD所在直线折叠,点C落在同一平面内,落点记为C′,BC′与AD交于点E,若AB=3,BC=4,则DE的长为$\frac{25}{8}$.
如图,将矩形ABCD沿对角线BD所在直线折叠,点C落在同一平面内,落点记为C′,BC′与AD交于点E,若AB=3,BC=4,则DE的长为$\frac{25}{8}$.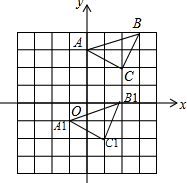 已知:△ABC在坐标平面内,三个顶点的坐标分别为A(0,3),B(3,4),C(2,2)(正方形网格中,每个小正方形的边长是1个单位长度),画出△ABC向下平移4个单位,再向左平移1个单位得到△A1B1C1,并直接写出C1点的坐标.
已知:△ABC在坐标平面内,三个顶点的坐标分别为A(0,3),B(3,4),C(2,2)(正方形网格中,每个小正方形的边长是1个单位长度),画出△ABC向下平移4个单位,再向左平移1个单位得到△A1B1C1,并直接写出C1点的坐标.