题目内容
17. 如图,直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于D,过D作DE⊥MN于E.
如图,直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于D,过D作DE⊥MN于E.(1)求证:DE是⊙O的切线;
(2)若∠EDA=30°,AD=6cm,求⊙O的半径.
分析 (1)连结OD,如图,由AD平分∠CAM得∠1=∠2,加上∠2=∠3,则∠1=∠3,于是可判断OD∥MN,由于DE⊥MN,所以OD⊥DE,则可根据切线的判定定理得到DE是⊙O的切线.
(2)依题意得到△ACD∽△ADE.根据相似三角形的性质列出比例式,代入数据即可求得圆的半径.
解答 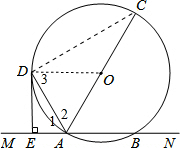 证明:(1)连结OD,如图,
证明:(1)连结OD,如图,
∵AD平分∠CAM,
∴∠1=∠2,
∵OA=OD,
∴∠2=∠3,
∴∠1=∠3,
∴OD∥MN,
∵DE⊥MN,
∴OD⊥DE,
∴DE是⊙O的切线.
(2)∵∠EDA=30°,AD=6cm,
∴AE=$\frac{1}{2}$AD=3cm.
连接CD.
∵AC是⊙O的直径,
∴∠ADC=∠AED=90°.
∵∠CAD=∠DAE,
∴△ACD∽△ADE.
∴$\frac{AD}{AE}$=$\frac{AC}{AD}$,即$\frac{6}{3}$=$\frac{AC}{6}$,
则AC=12(cm).
∴⊙O的半径是6cm.
点评 本题考查常见的几何题型,包括切线的判定,线段等量关系的证明及线段长度的求法,要求学生掌握常见的解题方法,并能结合图形选择简单的方法解题.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
 已知二次函数y=x2-4x+3.
已知二次函数y=x2-4x+3. 如图,在△ABC中,∠C=90°,sinA=$\frac{2}{5}$,D为AC上一点,∠BDC=45°,DC=6,求AD的长.
如图,在△ABC中,∠C=90°,sinA=$\frac{2}{5}$,D为AC上一点,∠BDC=45°,DC=6,求AD的长. 已知一次函数y=2x-3.
已知一次函数y=2x-3.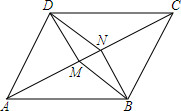 如图:已知?ABCD中,DM⊥AC于M,BN⊥AC于N,求证:四边形DMBN为平行四边形.
如图:已知?ABCD中,DM⊥AC于M,BN⊥AC于N,求证:四边形DMBN为平行四边形.