题目内容
8.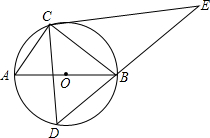 如图,定点C、动点D在⊙O上,并且位于直径AB的两侧,AB=5,AC=3,过点C在作CE⊥CD交DB的延长线于点E,则线段CE长度的最大值为( )
如图,定点C、动点D在⊙O上,并且位于直径AB的两侧,AB=5,AC=3,过点C在作CE⊥CD交DB的延长线于点E,则线段CE长度的最大值为( )| A. | 5 | B. | 8 | C. | $\frac{32}{5}$ | D. | $\frac{20}{3}$ |
分析 当CD是直径时,CE最长,由AB是直径,得到∠ACB=90°,利用勾股定理得出BC的长度,又因为∠A=∠D,∠ABC=∠ACE=90°,推出△ABC∽△DCE,根据相似三角形的性质列方程求解.
解答 解:当CD是直径时,CE最长,
∵AB是直径,
∴∠ACB=90°,
∴BC=$\sqrt{A{B}^{2}-A{C}^{2}}=\sqrt{{5}^{2}-{3}^{2}}=4$,
∵∠A=∠D,∠ABC=∠ACE=90°,
∴△ABC∽△DCE,
∴$\frac{AC}{CD}=\frac{BC}{CE}$,
即$\frac{3}{5}=\frac{4}{CE}$,
∴CE=$\frac{20}{3}$,
故选:D.
点评 本题考查了相似三角形的判定和性质,圆周角定理,解直角三角形,勾股定理的应用,确定CE什么时候取最大值是解题的关键.

练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
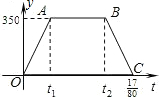 沪杭高速铁路已建成通车,某校研究性学习小组以此为课题,在研究列车的行驶速度时,得到一个数学问题.如图,若v是关于t的函数,图象为折线O-A-B-C,其中A(t1,350),B(t2,350),C($\frac{17}{80}$,0),四边形OABC的面积为70,则t2-t1=$\frac{3}{16}$.
沪杭高速铁路已建成通车,某校研究性学习小组以此为课题,在研究列车的行驶速度时,得到一个数学问题.如图,若v是关于t的函数,图象为折线O-A-B-C,其中A(t1,350),B(t2,350),C($\frac{17}{80}$,0),四边形OABC的面积为70,则t2-t1=$\frac{3}{16}$.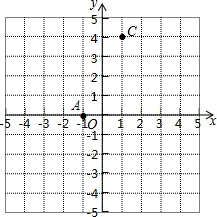 如图,A(-1,0),C(1,4),点B在x轴上,且AB=3.
如图,A(-1,0),C(1,4),点B在x轴上,且AB=3.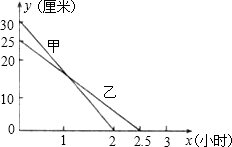 在一次蜡烛燃烧试验中,甲、乙两根蜡烛燃烧时剩余部分的高度y(厘米)与燃烧时间x(小时)之间的关系如图所示,请根据图象所提供的信息解答下列问题:
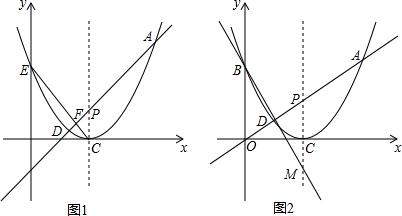
在一次蜡烛燃烧试验中,甲、乙两根蜡烛燃烧时剩余部分的高度y(厘米)与燃烧时间x(小时)之间的关系如图所示,请根据图象所提供的信息解答下列问题: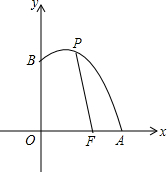 如图,已知点F的坐标为(3,0),点A,B分别是某函数图象与x轴、y轴的交点,P是此图象上的一动点.设P的横坐标为x,PF的长为d,且d与x之间满足关系:d=5-$\frac{3}{5}x$(0≤x≤5),给出以下四个结论:
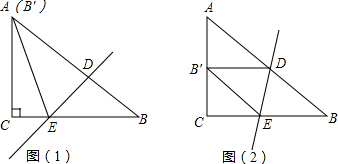
如图,已知点F的坐标为(3,0),点A,B分别是某函数图象与x轴、y轴的交点,P是此图象上的一动点.设P的横坐标为x,PF的长为d,且d与x之间满足关系:d=5-$\frac{3}{5}x$(0≤x≤5),给出以下四个结论: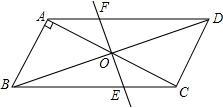 已知,如图?ABCD中,AB⊥AC,AB=1,BC=$\sqrt{5}$,对角线AC、BD交于0点,将直线AC绕点0顺时针旋转,分别交BC、AD于点E、F
已知,如图?ABCD中,AB⊥AC,AB=1,BC=$\sqrt{5}$,对角线AC、BD交于0点,将直线AC绕点0顺时针旋转,分别交BC、AD于点E、F