题目内容
 如图,点E、F在BC上,BE=CF,∠A=∠D,∠B=∠C,AF与DE交于点O.
如图,点E、F在BC上,BE=CF,∠A=∠D,∠B=∠C,AF与DE交于点O.(1)求证:AB=DC;
(2)若∠EOF=60°试判断△OEF的形状,并说明理由.
考点:全等三角形的判定与性质,等边三角形的判定与性质
专题:
分析:(1)易证BF=CE,即可求得△ABF≌△DCE,即可解题;
(2)根据(1)中求证的△ABF≌△DCE,即可求得∠OEF=∠OFE,即可解题.
(2)根据(1)中求证的△ABF≌△DCE,即可求得∠OEF=∠OFE,即可解题.
解答:解:(1)∵BE=CF,
∴BF=CE,
在△ABF和△DCE中,
,
∴△ABF≌△DCE,(AAS)
∴AB=DC;
(2)∵△ABF≌△DCE,
∴∠OEF=∠OFE,
∵∠EOF=60°,
∴∠OEF=∠OFE=∠EOF=60°,
∴△OEF为等边三角形.
∴BF=CE,
在△ABF和△DCE中,
|
∴△ABF≌△DCE,(AAS)
∴AB=DC;
(2)∵△ABF≌△DCE,
∴∠OEF=∠OFE,
∵∠EOF=60°,
∴∠OEF=∠OFE=∠EOF=60°,
∴△OEF为等边三角形.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边、对应角相等的性质,考查了等边三角形的判定,本题中求证△ABF≌△DCE是解题的关键.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
如果x:y=2:3,则下列各式不成立的是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知,E(-4,4)、F(-2,-2),以O为位似中心,按1:2的比例尺把△EOF缩小,则点E的对应点E′的坐标为( )
| A、(2,-2) |
| B、(-2,2) |
| C、(2,-2)或(-2,2) |
| D、(8,-8)或(-8,8) |

 已知CD⊥AB于D,BE⊥AC于E 求证:D,B,C,E在同一圆上.
已知CD⊥AB于D,BE⊥AC于E 求证:D,B,C,E在同一圆上. 如图,圆内接四边形ABCD,两组对边的延长线分别相交于点E、F,且∠E=40°,∠F=60°,求∠A的度数.
如图,圆内接四边形ABCD,两组对边的延长线分别相交于点E、F,且∠E=40°,∠F=60°,求∠A的度数.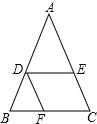 如图所示,已知DE∥BC,DF∥AC,且AE=3,AC=5,BC=10,求BF的长.
如图所示,已知DE∥BC,DF∥AC,且AE=3,AC=5,BC=10,求BF的长.