题目内容
如图，正方形网格中每个小正方形边长都是1，小正方形的顶点称为格点，在正方形网格中分别画出下列图形：
（1）长为
的线段PQ，其中P、Q都在格点上；
（2）面积为13的正方形ABCD，其中A、B、C、D都在格点上．
（1）长为
| 10 |
（2）面积为13的正方形ABCD，其中A、B、C、D都在格点上．
考点：勾股定理
专题：作图题
分析：（1）由勾股定理可知当直角边为1和3时，则斜边为
，由此可得线段PQ；
（2）由勾股定理可知当直角边为2和3时，则斜边为
，把斜边作为正方形的边长即可得到面积为13的正方形ABCD．
| 10 |
（2）由勾股定理可知当直角边为2和3时，则斜边为
| 13 |
解答：解：（1）（2）如图所示：
点评：本题考查了勾股定理的运用，本题需仔细分析题意，结合图形，利用勾股定理即可解决问题．
练习册系列答案
相关题目
若x=-6是关于x的方程
-（m-x）=1的解，则m的值为（ ）
| x |
| 3 |
| A、3 | B、9 | C、-9 | D、-3 |
如图，一个长方形花坛的长AD为8米，一条对角线AC的长为10米．把分式
中的a、b都扩大为原来的3倍，则分式的值（ ）
| ab |
| a+b |
| A、扩大为原来的6倍 | ||
| B、不变 | ||
C、缩小为原来的
| ||
| D、扩大为原来的3倍 |
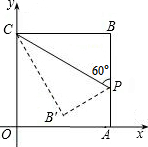如图，平面直角坐标系中，四边形OABC是正方形，点A的坐标是（4，0），点P为边AB上一点，沿CP折叠正方形，折叠后的点B落在平面内的点B′处，已知直线CB′的解析式为y=-
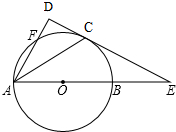如图，AB是圆O的直径，C是圆O上一点，直线CE与AB的延长线相交于E，AD⊥CE，垂足为D，AD交圆O于点F，AC平分∠DAE，若
如图，点E、F在BC上，BE=CF，∠A=∠D，∠B=∠C，AF与DE交于点O．