题目内容
2.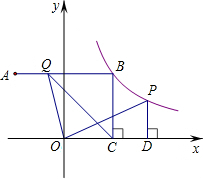 在平面直角坐标系中,点A(-3,4)关于y轴的对称点为点B,连接AB,反比例函数y=$\frac{k}{x}$(x>0)的图象经过点B,过点B作BC⊥x轴于点C,点P是该反比例函数图象上任意一点,过点P作PD⊥x轴于点D,点Q是线段AB上任意一点,连接OQ、CQ.
在平面直角坐标系中,点A(-3,4)关于y轴的对称点为点B,连接AB,反比例函数y=$\frac{k}{x}$(x>0)的图象经过点B,过点B作BC⊥x轴于点C,点P是该反比例函数图象上任意一点,过点P作PD⊥x轴于点D,点Q是线段AB上任意一点,连接OQ、CQ.(1)点B的坐标是(3,4);k的值为12.
(2)判断△QOC与△POD的面积是否相等,并说明理由.
分析 (1)根据点B与点A关于y轴对称,求出B点坐标,再代入反比例函数解析式解可求出k的值;
(2)设点P的坐标为(m,n),点P在反比例函数y=$\frac{12}{x}$(x>0)的图象上,求出S△POD,根据AB∥x轴,OC=3,BC=4,点Q在线段AB上,求出S△QOC即可.
解答  解:(1)∵点B与点A关于y轴对称,A(-3,4),
解:(1)∵点B与点A关于y轴对称,A(-3,4),
∴点B的坐标为(3,4),
∵反比例函数y=$\frac{k}{x}$(x>0)的图象经过点B.
∴$\frac{k}{3}$=4,
解得k=12.
故答案为(3,4),12;
(2)相等.理由如下:
设点P的坐标为(m,n),其中m>0,n>0,
∵点P在反比例函数y=$\frac{12}{x}$(x>0)的图象上,
∴n=$\frac{12}{m}$,即mn=12.
∴S△POD=$\frac{1}{2}$OD•PD=$\frac{1}{2}$mn=$\frac{1}{2}$×12=6,
∵A(-3,4),B(3,4),
∴AB∥x轴,OC=3,BC=4,
∵点Q在线段AB上,
∴S△QOC=$\frac{1}{2}$OC•BC=$\frac{1}{2}$×3×4=6.
∴S△QOC=S△POD.
点评 本题考查了关于y轴对称的点的坐标特征,反比例函数比例系数k的几何意义,反比例函数图象上点的坐标特征等知识,求出反比例函数解析式是解题的关键.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
10.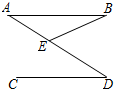 如图,直线AB∥CD,若∠B=24°,∠D=33°,则∠BED等于( )
如图,直线AB∥CD,若∠B=24°,∠D=33°,则∠BED等于( )
 如图,直线AB∥CD,若∠B=24°,∠D=33°,则∠BED等于( )
如图,直线AB∥CD,若∠B=24°,∠D=33°,则∠BED等于( )| A. | 24° | B. | 33° | C. | 57° | D. | 67° |
17.武汉市在一次扶贫助残活动中,捐款约5180000元,请将5180000元用科学记数法表示为( )
| A. | 0.518×107元 | B. | 5.18×106元 | C. | 51.8×105元 | D. | 518×104元 |
11.若4x2+mx+1是完全平方式,则m的值是( )
| A. | 4 | B. | -4 | C. | ±2 | D. | ±4 |
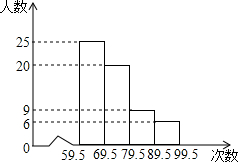 如图是九年级(1)班同学的一次体检每分钟心跳次数的频数分布直方图(次数均为整数).已知该班只有5位同学的心跳每分钟75次.请观察图回答:
如图是九年级(1)班同学的一次体检每分钟心跳次数的频数分布直方图(次数均为整数).已知该班只有5位同学的心跳每分钟75次.请观察图回答: 将两块全等的含30°角的三角尺按如图的方式摆放在一起.求证:四边形ABCD是平行四边形.
将两块全等的含30°角的三角尺按如图的方式摆放在一起.求证:四边形ABCD是平行四边形. 甲乙两人共同加工一批零件,从工作开始到加工完这批零件两人恰好同时工作6小时,二人各自加工零件的个数y(个)与加工时间x(小时)之间的函数图象如图所示,根据信息回答下列问题:
甲乙两人共同加工一批零件,从工作开始到加工完这批零件两人恰好同时工作6小时,二人各自加工零件的个数y(个)与加工时间x(小时)之间的函数图象如图所示,根据信息回答下列问题: