题目内容
19．在Rt△ABC中，∠C=90°，∠A=32°，AB=6，求AC、BC的长．（注：sin32°=0.530，cos32°=0.848，tan32°=0.625）分析 由∠C=90°，于是得到sinA=$\frac{BC}{AB}$，代入数据求得BC=3.180，由于cosA=$\frac{AC}{AB}$，代入数据求得AC=5.086．
解答 解：∵∠C=90°，
∴sinA=$\frac{BC}{AB}$，
即 sin32°=$\frac{BC}{6}$=0.530，
∴BC=3.180，
∵cosA=$\frac{AC}{AB}$，
即cos32°=$\frac{AC}{6}$=0.848，
∴AC=5.086．
点评 本题考查了解直角三角形，锐角三角函数的概念，熟记锐角三角函数的定义是解题的关键．
练习册系列答案
相关题目
如图，无盖的长方体盒子的长为15，宽为10，高为8，在顶点B处（盒子里面）有一滴蜂蜜，一只蚂蚁在顶点A处，想从盒子的A点爬到盒子的B点，爬行的最短路程是$\sqrt{529}$cm．
下面的哪个平面图形绕轴旋转一周得到的几何体从上面看到的如图所示（ ）
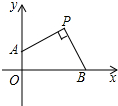如图，已知P（2，2），点B、A分别在x轴正半轴和y轴正半轴上，∠APB=90°，则OA+OB=4．
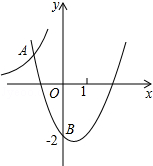如图，二次函数y=x2+bx+c的图象过点B（0，-2）．它与反比例函数y=-$\frac{12}{x}$的图象交于点A（m，4），求这个二次函数的解析式．
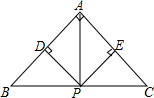在△ABC，点P是BC边的中点，PD⊥AB于点D，PE⊥AC于点E，求证：
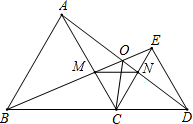如图，已知△ABC和△CDE均是等边三角形，点B、C、D在同一条直线上，BE与AD交于点O，AD与CE交于点N，AC与BE交于点M，连OC、MN，则下列结论①AD=BE；②AN=BM；③MN∥BD；④∠BOC=∠DOC；⑤若∠ADE=20°，则∠BED=100°；⑥OB=AO+OC，其中正确的结论个数有（ ）