题目内容
1．
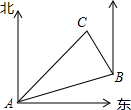同学甲要从A点出发到距离A点1000米的C地去，他先沿北偏东70°方向到达B地，然后再沿北偏西20°方向走了600米到达目的地C，由此可知AB之间的距离为（ ）| A． | 700米 | B． | 700$\sqrt{3}$米 | C． | 800米 | D． | 800$\sqrt{3}$米 |
分析 利用方向角得出∠1，∠2的度数，进而得出∠ABC的度数，再利用勾股定理得出AB的长．
解答 
解：∵同学甲沿北偏东70°方向到达B地，
∴∠2=70°，
∵沿北偏西20°方向走了600米到达目的地C，
∴∠1=20°，
∴∠ABC=90°，
∴在Rt△ABC中
AB=$\sqrt{A{C}^{2}-B{C}^{2}}$=$\sqrt{100{0}^{2}-60{0}^{2}}$=800（m）．
故选：C．
点评 此题主要考查了勾股定理以及方向角，根据题意得出∠ABC的度数是解题关键．
练习册系列答案
相关题目
11．在Rt△ABC中，∠C=90°，AB=2BC，那么sinA的值为（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{\sqrt{2}}{2}$ | C． | $\frac{\sqrt{3}}{2}$ | D． | 1 |
12．在实数0，π，$\frac{12}{11}$，-$\sqrt{4}$，$\sqrt{3}$中，是无理数的有（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
如图，无盖的长方体盒子的长为15，宽为10，高为8，在顶点B处（盒子里面）有一滴蜂蜜，一只蚂蚁在顶点A处，想从盒子的A点爬到盒子的B点，爬行的最短路程是$\sqrt{529}$cm．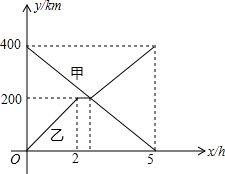
甲、乙两辆汽车分别从A、B两地同时出发，沿同一条公路相向而行，乙车车发2h后休息，与甲车相遇后，继续行驶，设甲、乙两车与B地的路程分别为y甲（km），y乙（km），甲车行驶的时间为x（h），y甲，y乙与x之间的函数图象如图所示，结合图象解答下列问题：
将一张长方形的纸片ABCD按如图所示方式折叠，使C点落在C′处，BC′交AD于点E，则△EBD的形状是等腰三角形．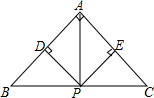
在△ABC，点P是BC边的中点，PD⊥AB于点D，PE⊥AC于点E，求证：