题目内容
17.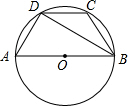 如图,AB是⊙O的直径,△BCD内接于⊙O,若AD=DC=5cm,∠CDB=30°,则四边形ABCD的周长为( )
如图,AB是⊙O的直径,△BCD内接于⊙O,若AD=DC=5cm,∠CDB=30°,则四边形ABCD的周长为( )| A. | 25cm | B. | 35cm | C. | 30cm | D. | 40cm |
分析 连接OD,OC,由AD=DC,根据在同圆中等弦对等弧,可得:$\widehat{AD}=\widehat{DC}$,根据等弧所对的圆心角相等,可得:∠AOD=∠DOC,然后根据圆周角定理可得:∠BOC=2∠BDC=60°,然后由∠AOD+∠DOC+∠BOC=180°,可得∠AOD=∠DOC=60°,进而可判断△AOD、△DOC、△BOC是等边三角形,从而可得:AD=DC=CB=OB=OA=5cm,进而可求四边形ABCD的周长.
解答 解:连接OD,OC,如图所示,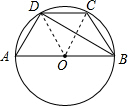
∵AD=DC,
∴$\widehat{AD}=\widehat{DC}$,
∴∠AOD=∠DOC,
∵∠BOC=2∠BDC,∠BDC=30°,
∴∠BOC=60°,
∵∠AOD+∠DOC+∠BOC=180°,
∴∠AOD=∠DOC=$\frac{180°-∠BOC}{2}$=60°,
∵OA=OD=OC=OB,
∴△AOD、△DOC、△BOC都是等边三角形,
∴AD=DC=CB=OB=OA=5cm,
∴四边形ABCD的周长=AD+DC+CB+OB+OA=5×5=25cm.
故选A.
点评 此题考查了圆周角定理,及弧、弦,圆心角之间的关系定理,解题的关键是:添加辅助线,判断△AOD、△DOC、△BOC是等边三角形.

练习册系列答案
相关题目
9.如果$\sqrt{\frac{5}{x-5}}$是二次根式,则x的取值范围( )
| A. | x≥5 | B. | x≤5 | C. | x>5 | D. | x<5 |
 如图,正方形A、B、C的边长分别为直角三角形的三边长,若正方形A、B的边长分别为8和12,则正方形C的面积为80.
如图,正方形A、B、C的边长分别为直角三角形的三边长,若正方形A、B的边长分别为8和12,则正方形C的面积为80.