题目内容
12.已知方程组$\left\{\begin{array}{l}{ax-by=4}\\{ax+by=0}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$,则3a-4b的值为11.分析 把x与y的值代入方程组,求出a与b的值,即可确定出3a-4b的值.
解答 解:把$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$代入得:$\left\{\begin{array}{l}{2a-b=4①}\\{2a+b=0②}\end{array}\right.$,
①+②得:4a=4,即a=1,
②-①得:2b=-4,即b=-2,
则3a-4b=3+8=11.
故答案为:11.
点评 此题考查了二元一次方程组的解,方程组的解即为能使方程组中两方程成立的未知数的值.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
17.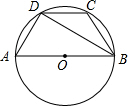 如图,AB是⊙O的直径,△BCD内接于⊙O,若AD=DC=5cm,∠CDB=30°,则四边形ABCD的周长为( )
如图,AB是⊙O的直径,△BCD内接于⊙O,若AD=DC=5cm,∠CDB=30°,则四边形ABCD的周长为( )
 如图,AB是⊙O的直径,△BCD内接于⊙O,若AD=DC=5cm,∠CDB=30°,则四边形ABCD的周长为( )
如图,AB是⊙O的直径,△BCD内接于⊙O,若AD=DC=5cm,∠CDB=30°,则四边形ABCD的周长为( )| A. | 25cm | B. | 35cm | C. | 30cm | D. | 40cm |
2.以下列各组数为边长,能构成直角三角形的是( )
| A. | 3,3,7 | B. | 3,5,8 | C. | 1.5,2,3 | D. | 6,8,10 |
 已知一次函数y=2x+b的图象如图所示,当x<0时,y的取值范围是y<-2.
已知一次函数y=2x+b的图象如图所示,当x<0时,y的取值范围是y<-2.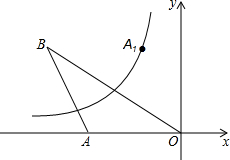 如图,在直角坐标系中,点A的坐标为(-10,0),点B在第二象限,AO=AB,OB=8$\sqrt{5}$,点A关于直线OB的对称点为A1,反比例函数y=$\frac{k}{x}$(k≠0,x<0)的图象经过点A1,则k=-48.
如图,在直角坐标系中,点A的坐标为(-10,0),点B在第二象限,AO=AB,OB=8$\sqrt{5}$,点A关于直线OB的对称点为A1,反比例函数y=$\frac{k}{x}$(k≠0,x<0)的图象经过点A1,则k=-48.