题目内容
12．作出函数y=$\frac{12}{x}$的图象，并根据图象回答下列问题：（1）当x=-2时，求y的值；
（2）当2＜y＜3是，求x的取值范围；
（3）当-4＜x＜-2时，求y的取值范围．
分析 （1）把x=-2代入解析式求得y的值；
（2）求得当y=2和y=3时函数值，根据函数图象的性质即可确定；
（3）求得当x=-4和x=-2时函数值，根据函数图象的性质即可确定．
解答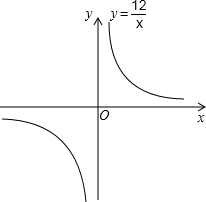 
解：（1）当x=-2时，y=$\frac{12}{-2}$=-6；
（2）当y=2时，x=$\frac{12}{2}$=6，当y=3时，x=$\frac{12}{3}$=4，
则x的范围是：4＜x＜6；
（3）当x=-4时，y=$\frac{12}{-4}$=-3，
当x=-2时，y=-6，
则y的范围是：-6＜y＜-3．
点评 本题考查了反比例函数的图象的性质，对于反比例函数y=$\frac{k}{x}$，当k＞0时，在每一个象限内，函数值y随自变量x的增大而减小；当k＜0时，在每一个象限内，函数值y随自变量x增大而增大．
练习册系列答案
黄冈天天练口算题卡系列答案
相关题目
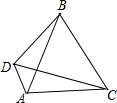在△ABC中，BC=BA，D是△ABC外一点，且∠BCD=∠BAD=60°，求证：BC=CD+DA．
如图，抛物线y=x2+m与x轴交于点A，B，与y轴交于点C，若∠ACB=90°，求抛物线的解析式．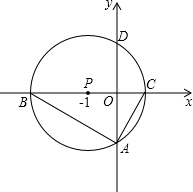
如图，以点P（-1，0）为圆心的圆，交x轴于B、C两点（B在C的左侧），交y轴于A、D两点（A在D的下方），AD=2，将△ABC绕点P旋转180°，得到△MCB．