题目内容
17．
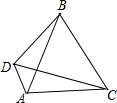在△ABC中，BC=BA，D是△ABC外一点，且∠BCD=∠BAD=60°，求证：BC=CD+DA．
分析 题目含有60°的特殊角，考虑运用余弦定理
解答 证明：在△BDC中，BD2=BC2+DC2-2BD•DC•cos∠BCD，
∵∠BCD=60°，
∴cos∠BCD=cos60°=$\frac{1}{2}$，即BD2=BC2+DC2-BC•DC，
在△BDA中，BD2=BA2+DA2-2BA•DA•cos∠BAD，
∵∠BAD=60°，
∴cos∠BAD=cos60°=$\frac{1}{2}$，即BD2=BA2+DA2-BA•DA，
∴BA2+DA2-BA•DA=BC2+DC2-BC•DC，
∵BC=AB，
∴DC2-BC•DC=DA2-BC•DA，即DC2-DA2=BC•DC-BC•DA，
∴（DC+DA）（DC-DA）=BC（DC-DA），
∴BC=DC+DA．
点评 本题考查了余弦定理及因式分解．熟记余弦定理是关键．
练习册系列答案
相关题目
8．关于x的方程mx2+（m-1）x+m=0有实根，则实数m的取值范围是（ ）
| A． | {m|-1＜m＜$\frac{1}{3}$} | B． | {m|-1≤m≤$\frac{1}{3}$} | C． | {m|-1≤m≤$\frac{1}{3}$且m≠0} | D． | {m|m≤-1或m≥$\frac{1}{3}$} |
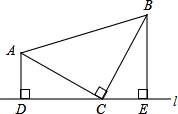如图，等腰直角三角形ABC中，∠ACB=90°，直线l经过点C（点A、B都在直线l的同侧），AD⊥l，BE⊥l，垂足分别为D、E，求证：△ADC≌△CEB．