题目内容
16. 如图,已知四边形ABCD中,∠B=∠C,AB=8,BC=10,CD=3,E是BC上一点,BE=4.
如图,已知四边形ABCD中,∠B=∠C,AB=8,BC=10,CD=3,E是BC上一点,BE=4.(1)求证:△ABE∽△ECD;
(2)求证:∠AED=∠B;
(3)已知点F在BC上,且∠AFD=∠AED.请画出∠AFD,并简要叙述画法,说明理由.
分析 (1)由AB=8,BC=10,CD=3,BE=4,易得AB:EC=BE:CD,又由∠B=∠C,即可证得:△ABE∽△ECD;
(2)由△ABE∽△ECD,可得∠BAE=∠CED,然后由三角形外角的性质,证得结论;
(3)根据同弧所对的圆周角相等,可得作△ADE的外接圆⊙O,则⊙O与BC的交点即为点F.
解答 证明:(1)∵BC=10,BE=4,
∴EC=BC-BE=6,
∵AB=8,CD=3,
∴AB:EC=8:6=4:3,BE:CD=4:3,
∴AB:EC=BE:CD,
∵∠B=∠C,
∴△ABE∽△ECD; (2)∵△ABE∽△ECD,
(2)∵△ABE∽△ECD,
∴∠BAE=∠CED,
∵∠B+∠BAE=∠AED+∠CED,
∴∠AED=∠B;
(3)如图,作△ADE的外接圆⊙O,则⊙O与BC的交点即为点F.
点评 此题考查了相似三角形的判定与性质以及圆周角的性质.注意有两边对应成比例且夹角相等三角形相似,同弧所对的圆周角相等.

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
6.以下列长度的三条线段为边,能构成三角形的( )
| A. | 7cm,8cm,15cm | B. | 15cm,20cm,5cm | C. | 6cm,7cm,5cm | D. | 7cm,6cm,14cm |
11.一枚质地均匀的正方体骰子六个面上的数字分别为1,2,3,4,5,6.掷四次骰子,依次得到朝上的面上的数字分别为a,b,c,d,则在a,a+b,a+b+c,a+b+c+d中存在一个数等于4的概率为( )
| A. | $\frac{33}{1296}$ | B. | $\frac{334}{1296}$ | C. | $\frac{343}{1296}$ | D. | $\frac{433}{1296}$ |
6.二次函数y=3x2-4的图象是一条抛物线,下列关于该抛物线的说法正确的是( )
| A. | 抛物线开口向下 | B. | 抛物线经过点(3,4) | ||
| C. | 抛物线的对称轴是直线x=1 | D. | 抛物线与x轴有两个交点 |
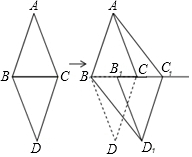 如图,△ABC和△DBC是两个具有公共边的全等三角形,AB=AC=6cm,BC=4cm,将△DBC沿射线BC平移一定的距离得到△D1B1C1,连接AC1,BD1.如果四边形ABD1C1是矩形,那么平移的距离为14cm.
如图,△ABC和△DBC是两个具有公共边的全等三角形,AB=AC=6cm,BC=4cm,将△DBC沿射线BC平移一定的距离得到△D1B1C1,连接AC1,BD1.如果四边形ABD1C1是矩形,那么平移的距离为14cm. 二次函数y=ax2+bx+c(a≠0)的图象如图,对称轴是x=1.下列结论:
二次函数y=ax2+bx+c(a≠0)的图象如图,对称轴是x=1.下列结论: 如图,△ABC是一块铁皮余料.已知底边BC=160cm,高AD=120cm.在铁皮余料上截取一个矩形EFGH,使点H在AB上,点G在AC上,点E、F在BC上,AD交HG于点M.
如图,△ABC是一块铁皮余料.已知底边BC=160cm,高AD=120cm.在铁皮余料上截取一个矩形EFGH,使点H在AB上,点G在AC上,点E、F在BC上,AD交HG于点M.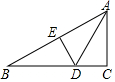 如图,在Rt△ABC中,∠C=90°,∠CAB的平分线交BC于D,DE是AB的垂直平分线,垂足为E,若BC=6,则DE的长为2.
如图,在Rt△ABC中,∠C=90°,∠CAB的平分线交BC于D,DE是AB的垂直平分线,垂足为E,若BC=6,则DE的长为2.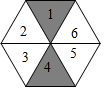 如图所示的六边形广场由若干个大小完全相同的正三角形组成,一只小鸟在广场上随机停留,刚好落在数字是5的三角形区域的概率为$\frac{1}{6}$.
如图所示的六边形广场由若干个大小完全相同的正三角形组成,一只小鸟在广场上随机停留,刚好落在数字是5的三角形区域的概率为$\frac{1}{6}$.