题目内容
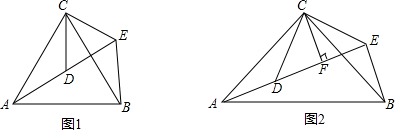
4. 二次函数y=ax2+bx+c(a≠0)的图象如图,对称轴是x=1.下列结论:
二次函数y=ax2+bx+c(a≠0)的图象如图,对称轴是x=1.下列结论:①abc>0
②2a+b=0
③4a+2b+c>0
其中正确的是②③.(填序号)
分析 根据抛物线的开口方向、对称轴及抛物线与y轴的交点可判断①;由抛物线的对称轴可判断②;根据抛物线的对称轴为x=1,且x=0时y>0可判断③.
解答 解:①∵抛物线的开口向上,
∴a>0,
∵x=-$\frac{b}{2a}$=1,
∴b=-2a<0,
∵抛物线与y轴的交点在正半轴,
∴当x=0时,y=c>0,
则abc<0,故此结论错误;
②∵x=-$\frac{b}{2a}$=1,
∴2a+b=0,故此结论正确;
③∵抛物线的对称轴为x=1,且x=1时y>0,
∴当x=2时,y=4a+2b+c>0,此结论正确;
故答案为:②③.
点评 本题考查了二次函数的图象与系数的关系,二次函数y=ax2+bx+c系数符号由抛物线开口方向、对称轴、抛物线与y轴的交点、抛物线与x轴交点的个数等确定.

练习册系列答案
相关题目
19.在同一平面直角坐标系内,将函数y=x2+4x+1的图象沿x轴向右平移2个单位长度后再沿y轴向下平移1个单位长度,得到图象的顶点坐标是( )
| A. | (-1,1) | B. | (0,-4) | C. | (2,-2) | D. | (1,-1) |
14. 如图,点C在线段AB上,D是线段AC的中点.若CB=2,CD=3CB,则线段AB的长为( )
如图,点C在线段AB上,D是线段AC的中点.若CB=2,CD=3CB,则线段AB的长为( )
 如图,点C在线段AB上,D是线段AC的中点.若CB=2,CD=3CB,则线段AB的长为( )
如图,点C在线段AB上,D是线段AC的中点.若CB=2,CD=3CB,则线段AB的长为( )| A. | 6 | B. | 10 | C. | 14 | D. | 18 |
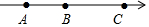 如图,已知数轴上A点表示数a,B点表示数b,C点表示数c.
如图,已知数轴上A点表示数a,B点表示数b,C点表示数c. 将如图所示的平面展开图折叠成正方体,则a对面的数字是-1.
将如图所示的平面展开图折叠成正方体,则a对面的数字是-1.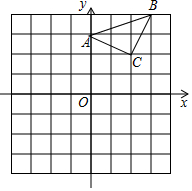 已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度). 如图,已知四边形ABCD中,∠B=∠C,AB=8,BC=10,CD=3,E是BC上一点,BE=4.
如图,已知四边形ABCD中,∠B=∠C,AB=8,BC=10,CD=3,E是BC上一点,BE=4.