题目内容
8.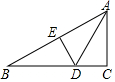 如图,在Rt△ABC中,∠C=90°,∠CAB的平分线交BC于D,DE是AB的垂直平分线,垂足为E,若BC=6,则DE的长为2.
如图,在Rt△ABC中,∠C=90°,∠CAB的平分线交BC于D,DE是AB的垂直平分线,垂足为E,若BC=6,则DE的长为2.
分析 由角平分线和线段垂直平分线的性质可求得∠B=∠CAD=∠DAB=30°,
解答 解:∵DE垂直平分AB,
∴DA=DB,
∴∠B=∠DAB,
∵AD平分∠CAB,
∴∠CAD=∠DAB,
∵∠C=90°,
∴3∠CAD=90°,
∴∠CAD=30°,
∵AD平分∠CAB,DE⊥AB,CD⊥AC,
∴CD=DE=$\frac{1}{2}$BD,
∵BC=6,
∴CD=DE=2,
故答案为:2.
点评 本题主要考查线段垂直平分线的性质,掌握线段垂直平分线上的点到线段两端点的距离相等是解题的关键.

练习册系列答案
相关题目
19.在同一平面直角坐标系内,将函数y=x2+4x+1的图象沿x轴向右平移2个单位长度后再沿y轴向下平移1个单位长度,得到图象的顶点坐标是( )
| A. | (-1,1) | B. | (0,-4) | C. | (2,-2) | D. | (1,-1) |
3.某单位向一所希望小学赠送1080件文具,现用A,B两种不同的包装箱进行包装,已知每个B型包装箱比A型包装箱多装15件文具,单独使用B型包装箱比单独使用A型包装箱可少用12个,设B型包装箱每个可以装x件文具,根究题意列方程为( )
| A. | $\frac{1080}{x}$=$\frac{1080}{x-15}$-12 | B. | $\frac{1080}{x}$=$\frac{1080}{x-15}$+12 | ||
| C. | $\frac{1080}{x}$=$\frac{1080}{x+15}$-12 | D. | $\frac{1080}{x}$=$\frac{1080}{x+15}$+12 |
17.如果两个相似三角形的面积比是1:4,那么它们的周长比是( )
| A. | 1:16 | B. | 1:6 | C. | 1:4 | D. | 1:2 |

 如图,已知四边形ABCD中,∠B=∠C,AB=8,BC=10,CD=3,E是BC上一点,BE=4.
如图,已知四边形ABCD中,∠B=∠C,AB=8,BC=10,CD=3,E是BC上一点,BE=4.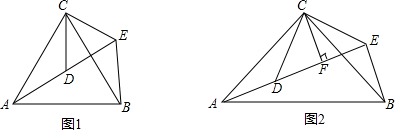
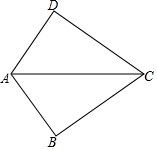 如图,△ABC≌△ADC,∠B=80°,则∠D的度数为80°.
如图,△ABC≌△ADC,∠B=80°,则∠D的度数为80°.