题目内容
 如图,正方形DEFG在等边三角形ABC的内部,点D、E分别在AB、BC上,且BD=BE.若AC=18,GF=6,则点F到AC的距离为( )
如图,正方形DEFG在等边三角形ABC的内部,点D、E分别在AB、BC上,且BD=BE.若AC=18,GF=6,则点F到AC的距离为( )| A、2 | ||
| B、3 | ||
C、12-4
| ||
D、6
|
考点:等边三角形的性质,含30度角的直角三角形,勾股定理
专题:
分析:过点B作BH⊥AC于H,交GF于K,根据等边三角形的性质求出∠A=∠ABC=60°,然后判定△BDE是等边三角形,再根据等边三角形的性质求出∠BDE=60°,然后根据同位角相等,两直线平行求出AC∥DE,再根据正方形的对边平行得到DE∥GF,从而求出AC∥DE∥GF,再根据等边三角形的边的与高的关系表示出KH,然后根据平行线间的距离相等即可得解.
解答: 解:如图,过点B作BH⊥AC于H,交GF于K,
解:如图,过点B作BH⊥AC于H,交GF于K,
∵△ABC是等边三角形,
∴∠A=∠ABC=60°,
∵BD=BE,
∴△BDE是等边三角形,
∴∠BDE=60°,
∴∠A=∠BDE,
∴AC∥DE,
∵四边形DEFG是正方形,GF=6,
∴DE∥GF,
∴AC∥DE∥GF,
∴KH=18×
-6×
-6=9
-3
-6=6
-6,
∴F点到AC的距离为6
-6.
故选D.
 解:如图,过点B作BH⊥AC于H,交GF于K,
解:如图,过点B作BH⊥AC于H,交GF于K,∵△ABC是等边三角形,
∴∠A=∠ABC=60°,
∵BD=BE,
∴△BDE是等边三角形,
∴∠BDE=60°,
∴∠A=∠BDE,
∴AC∥DE,
∵四边形DEFG是正方形,GF=6,
∴DE∥GF,
∴AC∥DE∥GF,
∴KH=18×
| ||
| 2 |
| ||
| 2 |
| 3 |
| 3 |
| 3 |
∴F点到AC的距离为6
| 3 |
故选D.
点评:本题考查了正方形的对边平行,四条边都相等的性质,等边三角形的判定与性质,等边三角形的高线等于边长的
倍,以及平行线间的距离相等的性质,综合题,但难度不大,熟记各图形的性质是解题的关键.
| ||
| 2 |

练习册系列答案
相关题目
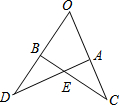 如图所示,OA=OB,OC=OD,∠O=50°,∠D=35°,则∠OBC的度数是( )
如图所示,OA=OB,OC=OD,∠O=50°,∠D=35°,则∠OBC的度数是( )| A、130° | B、85° |
| C、105° | D、95° |
X<0,Y>0时,则X,X+Y,X-Y,Y中最小的数是( )
| A、X-Y | B、Y | C、X+Y | D、X |
下列说法:
①角平分线上的点到角两边的距离相等;
②等腰三角形的高、中线、角平分线互相重合;
③三角形三边的垂直平分线交于一点且这一点到三角形三个顶点的距离相等;
④等腰三角形的一边长为8,一边长为16,那么它的周长是32或40.
其中,所有正确说法的序号是( )
①角平分线上的点到角两边的距离相等;
②等腰三角形的高、中线、角平分线互相重合;
③三角形三边的垂直平分线交于一点且这一点到三角形三个顶点的距离相等;
④等腰三角形的一边长为8,一边长为16,那么它的周长是32或40.
其中,所有正确说法的序号是( )
| A、①②③ | B、②③④ |
| C、①③ | D、②④ |
 如图,五边形ABCDE和五边形A1B1C1D1E1是位似图形,点A和点A1是一对对应点,P是位似中心,且2PA=3PA1,则五边形ABCDE和五边形A1B1C1D1E1的相似比等于( )
如图,五边形ABCDE和五边形A1B1C1D1E1是位似图形,点A和点A1是一对对应点,P是位似中心,且2PA=3PA1,则五边形ABCDE和五边形A1B1C1D1E1的相似比等于( )A、
| ||
B、
| ||
C、
| ||
D、
|
已知方程3x-m=
与方程x+4=0的解相同,则m的值为( )
| m+3x |
| 2 |
| A、-18 | B、18 |
| C、-4 | D、-12 |
 如图,点D在△ABC的边AC上,添加下列哪个条件后,仍无法判定△ABC∽△ADB( )
如图,点D在△ABC的边AC上,添加下列哪个条件后,仍无法判定△ABC∽△ADB( )A、
| ||||
B、
| ||||
| C、∠C=∠ABD | ||||
| D、∠CBA=∠ADB |