题目内容
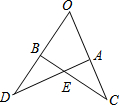 如图所示,OA=OB,OC=OD,∠O=50°,∠D=35°,则∠OBC的度数是( )
如图所示,OA=OB,OC=OD,∠O=50°,∠D=35°,则∠OBC的度数是( )| A、130° | B、85° |
| C、105° | D、95° |
考点:全等三角形的判定与性质
专题:
分析:易证△OAD≌△OBC,可得∠OBC=∠OAD,根据三角形内角和为180°即可解题.
解答:解:∵在△OAD和△OBC中,
,
∴△OAD≌△OBC,(SAS)
∴∠OBC=∠OAD=180°-∠O-∠D=95°,
故选D.
|
∴△OAD≌△OBC,(SAS)
∴∠OBC=∠OAD=180°-∠O-∠D=95°,
故选D.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△OAD≌△OBC是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
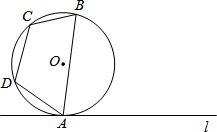 如图,⊙O的半径为3,四边形ABCD是⊙O的内接四边形,直线l与⊙O相切于点A,若∠A=60°,∠D=110°,
如图,⊙O的半径为3,四边形ABCD是⊙O的内接四边形,直线l与⊙O相切于点A,若∠A=60°,∠D=110°, |
| CD |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知△ABC的三边长分别为1、5、x,周长为整数,则△ABC的形状是( )
| A、直角三角形 |
| B、等腰三角形 |
| C、等腰直角三角形 |
| D、等边三角形 |
 如图,正方形DEFG在等边三角形ABC的内部,点D、E分别在AB、BC上,且BD=BE.若AC=18,GF=6,则点F到AC的距离为( )
如图,正方形DEFG在等边三角形ABC的内部,点D、E分别在AB、BC上,且BD=BE.若AC=18,GF=6,则点F到AC的距离为( )| A、2 | ||
| B、3 | ||
C、12-4
| ||
D、6
|
 如图,求△AOB的面积.
如图,求△AOB的面积. 如图,P是直线y=-x+4上的一点,以点P为圆心,1个单位长度为半径作⊙P,当⊙P与x轴相切,点P的坐标为
如图,P是直线y=-x+4上的一点,以点P为圆心,1个单位长度为半径作⊙P,当⊙P与x轴相切,点P的坐标为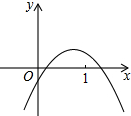 二次函数y=ax2+bx+c的图象如图所示,则下面正确的结论有( )
二次函数y=ax2+bx+c的图象如图所示,则下面正确的结论有( )