题目内容
下列说法:
①角平分线上的点到角两边的距离相等;
②等腰三角形的高、中线、角平分线互相重合;
③三角形三边的垂直平分线交于一点且这一点到三角形三个顶点的距离相等;
④等腰三角形的一边长为8,一边长为16,那么它的周长是32或40.
其中,所有正确说法的序号是( )
①角平分线上的点到角两边的距离相等;
②等腰三角形的高、中线、角平分线互相重合;
③三角形三边的垂直平分线交于一点且这一点到三角形三个顶点的距离相等;
④等腰三角形的一边长为8,一边长为16,那么它的周长是32或40.
其中,所有正确说法的序号是( )
| A、①②③ | B、②③④ |
| C、①③ | D、②④ |
考点:角平分线的性质,线段垂直平分线的性质,等腰三角形的性质
专题:
分析:根据角平分线的性质判断①;根据等腰三角形三线合一的性质判断②;根据线段垂直平分线的性质判断③;根据等腰三角形的性质、三角形三边关系及周长的定义判断④.
解答:解:①角平分线上的点到角两边的距离相等,说法正确;
②等腰三角形底边上的高、中线与顶角的角平分线互相重合,说法错误;
③三角形三边的垂直平分线交于一点且这一点到三角形三个顶点的距离相等,说法正确;
④等腰三角形的一边长为8,一边长为16,那么它的周长是40.
故选C.
②等腰三角形底边上的高、中线与顶角的角平分线互相重合,说法错误;
③三角形三边的垂直平分线交于一点且这一点到三角形三个顶点的距离相等,说法正确;
④等腰三角形的一边长为8,一边长为16,那么它的周长是40.
故选C.
点评:本题考查了角平分线的性质,等腰三角形的性质,线段垂直平分线的性质,三角形三边关系定理,熟记性质与定理是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知一个多边形的内角和与外角和的比是9:2,则这个多边形的边数是( )
| A、9 | B、10 | C、11 | D、12 |
 如图,正方形DEFG在等边三角形ABC的内部,点D、E分别在AB、BC上,且BD=BE.若AC=18,GF=6,则点F到AC的距离为( )
如图,正方形DEFG在等边三角形ABC的内部,点D、E分别在AB、BC上,且BD=BE.若AC=18,GF=6,则点F到AC的距离为( )| A、2 | ||
| B、3 | ||
C、12-4
| ||
D、6
|
已知(5,-1)是双曲线y=
(k≠0)上的一点,则下列各点中不在该图象上的是( )
| k |
| x |
A、(
| ||
| B、(5,1) | ||
| C、(-1,5) | ||
D、(10,-
|
将一元一次方程3x2-1=6x化成一般形式后,二次项系数和一次项系数分别为( )
| A、3,-6 |
| B、3,6 |
| C、3,-1 |
| D、3x2,-6x |
 如图,P是直线y=-x+4上的一点,以点P为圆心,1个单位长度为半径作⊙P,当⊙P与x轴相切,点P的坐标为
如图,P是直线y=-x+4上的一点,以点P为圆心,1个单位长度为半径作⊙P,当⊙P与x轴相切,点P的坐标为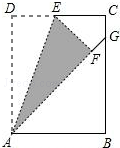 如图,在矩形ABCD中,点E是边CD的中点,AB=2,AD=3,将△ADE沿AE折叠后得到△AFE,且点F在矩形ABCD内部,将AF延长交边BC于点C,则CG的长为
如图,在矩形ABCD中,点E是边CD的中点,AB=2,AD=3,将△ADE沿AE折叠后得到△AFE,且点F在矩形ABCD内部,将AF延长交边BC于点C,则CG的长为 如图,在长方形网格中,每个小长方形的长为2,宽为1,A、B两点在网格格点上,以A、B、C为顶点的三角形面积为2,则满足条件的点C的个数是( )
如图,在长方形网格中,每个小长方形的长为2,宽为1,A、B两点在网格格点上,以A、B、C为顶点的三角形面积为2,则满足条件的点C的个数是( )