题目内容
2. 如图,在矩形ABCD中.点O在边AB上,∠AOC=∠BOD.求证:AO=OB.
如图,在矩形ABCD中.点O在边AB上,∠AOC=∠BOD.求证:AO=OB.
分析 首先根据矩形的性质得到∠A=∠B=90°,AD=BC,利用角之间的数量关系得到∠AOD=∠BOC,利用AAS证明△AOD≌△BOC,即可得到AO=OB.
解答 解:∵四边形ABCD是矩形,
∴∠A=∠B=90°,AD=BC,
∵∠AOC=∠BOD,
∴∠AOC-∠DOC=∠BOD-∠DOC,
∴∠AOD=∠BOC,
在△AOD和△BOC中,
$\left\{\begin{array}{l}{∠A=∠B}\\{∠AOD=∠BOC}\\{AD=BC}\end{array}\right.$,
∴△AOD≌△BOC,
∴AO=OB.
点评 本题主要考查了矩形的性质的知识,解答本题的关键是证明△AOD≌△BOC,此题难度不大.

练习册系列答案
相关题目
11. 如图是由七个棱长为1的正方体组成的一个几何体,其俯视图的面积是( )
如图是由七个棱长为1的正方体组成的一个几何体,其俯视图的面积是( )
 如图是由七个棱长为1的正方体组成的一个几何体,其俯视图的面积是( )
如图是由七个棱长为1的正方体组成的一个几何体,其俯视图的面积是( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
1.某校初一年级为了解学生课堂发言情况,随机抽取该年级部分学生,对他们某天在课堂上发言的次数进行了统计,其结果如下表,并绘制了如图所示的两幅不完整的统计图,已知B、E两组发言人数的比为5;2,请结合图中相关数据回答下列问题:

(1)求出样本容量,并补全直方图(在图中标出各组人数);
(2)课堂发言次数的中位数落在哪个组;
(3)该年级共有学生500人,请估计全年级在这天里发言次数不少于12次的人数.

(1)求出样本容量,并补全直方图(在图中标出各组人数);
(2)课堂发言次数的中位数落在哪个组;
(3)该年级共有学生500人,请估计全年级在这天里发言次数不少于12次的人数.
| 组别 | 课堂发言次数n |
| A | 0≤n<3 |
| B | 3≤n<6 |
| C | 6≤n<9 |
| D | 9≤n<12 |
| E | 12≤n<15 |
| F | 15≤n<18 |
 在矩形ABCD中,AB=5,AD=12,将矩形ABCD沿直线l向右翻滚两次至如图所示位置,则点B所经过的路线长是12.5π(结果不取近似值).
在矩形ABCD中,AB=5,AD=12,将矩形ABCD沿直线l向右翻滚两次至如图所示位置,则点B所经过的路线长是12.5π(结果不取近似值). 如图,在平行四边形ABCD中,EF∥AB交AD于E,交BD于F,DE:EA=3:4,EF=3,则CD的长为( )
如图,在平行四边形ABCD中,EF∥AB交AD于E,交BD于F,DE:EA=3:4,EF=3,则CD的长为( ) 一块直角三角板ABC按如图放置,顶点A的坐标为(0,1),直角顶点C的坐标为(-3,0),∠B=30°,则点B的坐标为(-3-$\sqrt{3}$,3$\sqrt{3}$).
一块直角三角板ABC按如图放置,顶点A的坐标为(0,1),直角顶点C的坐标为(-3,0),∠B=30°,则点B的坐标为(-3-$\sqrt{3}$,3$\sqrt{3}$). 如图,一只蚂蚁沿着棱长为2的正方体表面从点A出发,经过3个面爬到点B,如果它运动的路径是最短的,则AC的长为$\frac{2\sqrt{10}}{3}$.
如图,一只蚂蚁沿着棱长为2的正方体表面从点A出发,经过3个面爬到点B,如果它运动的路径是最短的,则AC的长为$\frac{2\sqrt{10}}{3}$.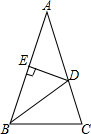 如图,在△ABC中,AB=AC,∠A=36°,BD为角平分线,DE⊥AB,垂足为E.
如图,在△ABC中,AB=AC,∠A=36°,BD为角平分线,DE⊥AB,垂足为E.